"/usr/lib/python3.6/site-packages/h5py/__init__.py:36: FutureWarning: Conversion of the second argument of issubdtype from `float` to `np.floating` is deprecated. In future, it will be treated as `np.float64 == np.dtype(float).type`.\n",
"/udd/kchoi/igrida/miniconda/envs/gpu/lib/python3.6/site-packages/h5py/__init__.py:36: FutureWarning: Conversion of the second argument of issubdtype from `float` to `np.floating` is deprecated. In future, it will be treated as `np.float64 == np.dtype(float).type`.\n",
" from ._conv import register_converters as _register_converters\n"
" from ._conv import register_converters as _register_converters\n"
"To have a more complex model that can do more usefull things, we can stack multiple neurons in parallel in order to make a *layer* of neurons.\n",
"To have a more complex model that can do more usefull things, we can stack multiple neurons in parallel in order to make a *layer* of neurons.\n",
"Then, when to connect multiple layers one after the other, you obtain what we call a Multi-Layered Perceptrons or MLP.\n",
"Then, when to connect multiple layers one after the other, you obtain what we call a Multi-Layered Perceptrons or MLP.\n",
"WARNING! Keep in mind that, even though we use Perceptron here, if you want to train this network, you will have to use a Sigmoid neuron or any kind of trainable neuron.\n",
"*WARNING*! Keep in mind that, even though we use Perceptron here, if you want to train this network, you will have to use a Sigmoid neuron or any kind of trainable neuron.\n",
"print(\"network weights and biases:\", variables)"
]
]
},
},
{
{
"cell_type": "markdown",
"cell_type": "markdown",
"metadata": {},
"metadata": {},
"source": [
"source": [
"## (Stochastic) Gradient Descent\n",
"\n",
"\n",
"Next, let's train this neuron so it will automatically adjust it's weights and bias to compute the NAND function.\n",
"As I said earlier, the secret magic sauce of Deep Learning training algorithm is the Gradient Descent algorithm.\n",
"The first and mother of all deep learning training algorithm is the gradient descent algorithm.\n",
"The Gradient Descent algorithm works on one example at a time.\n",
"Instead, the Stochastic Gradient Descent works on a *mini-batch* of examples at a time.\n",
"\n",
"\n",
"First, we will need a cost function (or loss function or objective function).\n",
"The goal of a training algorithm is to tune the weights and biases in order to minimize a *cost function*.\n",
"A cost function is a function that tells us how good or bad we are doing.\n",
"A cost function is a function that tells us how good or bad we are doing.\n",
"You can see the cost function as a distance computation between the output of our neurone and the real value we wanted our network to output.\n",
"You can see the cost function as a distance computation between the output of our neurone and the real value we wanted our network to output.\n",
"Traditionnally, the quadratic cost function is used in gradient descent tutorial because it's super easy to differentiate:\n",
"Traditionnally, the quadratic cost function, also called Mean Squared Error (MSE) is used in gradient descent tutorial because it's super easy to differentiate:\n",
"\n",
"\n",
"$$\n",
"$$\n",
"C(w, b) = {1 \\over 2} \\|real\\_output(x) - neurone\\_output(x)\\|^{2}\n",
"C(w, b) = {1 \\over 2n} \\sum_{x}\\|real\\_output(x) - network\\_output(x)\\|^{2}\n",
"$$"
"$$\n",
"\n",
"Here, $w$ denotes the collection of all weights in the network, $b$ all the biases, $n$ is the total number of training inputs, $network\\_output(x)$ is the vector of outputs from the network when $x$ is input, and the sum is over all training inputs, $x$.\n",
"\n",
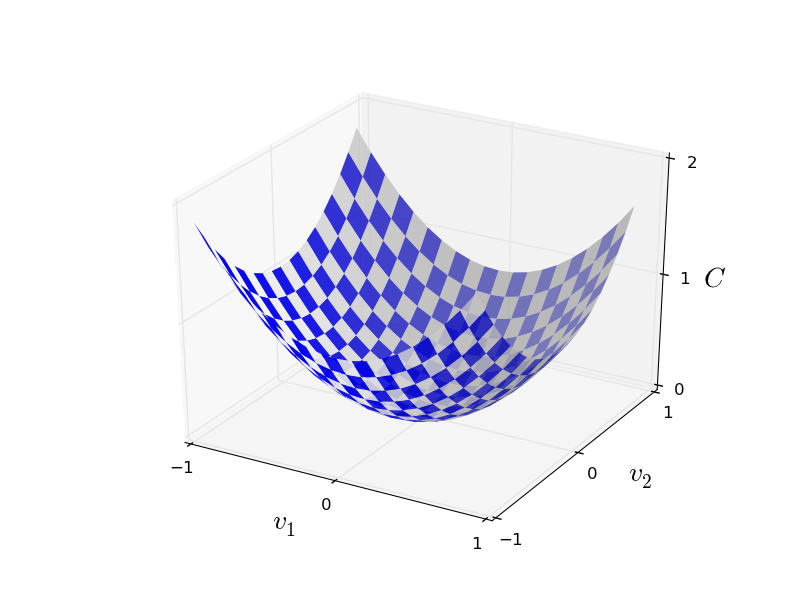
"In order to visualize how gradient descent works, imagine you have two weights: $v_{1}$ and $v_{2}$.\n",
"When using the MSE cost function, you can visualize it as a convexe plane where you want to find the minimum of this plane.\n",
"\n",
"\n",
"\n",
"Imagine that the current state of your network (with all of its weights and biases) is represented by a point on this plane.\n",
"If you can compute the gradient for all weights and biases, you then know in which direction to go in order to find the minimum of this plane.\n",
"categorical cross-entropy cost function: Measures the probability error in discrete classification tasks in which the classes are mutually exclusive (each entry is in exactly one class).\n",
"\n",
"### using MLP\n",
"\n",
"The code comes entirely from this keras examples: https://github.com/keras-team/keras/blob/master/examples/mnist_mlp.py"
]
]
},
},
{
{
"cell_type": "code",
"cell_type": "code",
"execution_count": 29,
"execution_count": 140,
"metadata": {},
"outputs": [
{
"name": "stderr",
"output_type": "stream",
"text": [
"Using TensorFlow backend.\n"
]
}
],
"source": [
"import keras\n",
"from keras.datasets import mnist\n",
"from keras.models import Sequential\n",
"from keras.layers import Dense, Dropout\n",
"from keras.optimizers import RMSprop"
]
},
{
"cell_type": "code",
"execution_count": 142,
"metadata": {},
"outputs": [],
"source": [
"# Here we declare some hyperparameters\n",
"batch_size = 128\n",
"# we have 10 class of digits 0...9\n",
"num_classes = 10\n",
"# One epoch consists of one full training cycle on the training set.\n",
"# Once every sample in the set is seen, you start again - marking the beginning of the 2nd epoch.\n",
"epochs = 20"
]
},
{
"cell_type": "code",
"execution_count": 151,
"metadata": {},
"outputs": [],
"source": [
"# loads the data\n",
"def load_mnist_mlp():\n",
" # the data, split between train and test sets\n",
In this tutorial, we will present some of the basic concept of what is a neuron, neural network and how to train it for some task like classification or regression.
In this tutorial, we will present some of the basic concept of what is a neuron, neural network and how to train it for some task like classification or regression.
Let's dive in.
Let's dive in.
This tutorial is (almost completely) inspired from this [online book](http://neuralnetworksanddeeplearning.com) which I found is a gold mine if you want to understand how neural networks work and how they are implemented.
This tutorial is (almost completely) inspired from this [online book](http://neuralnetworksanddeeplearning.com) which I found is a gold mine if you want to understand how neural networks work and how they are implemented.
## Perceptrons and Sigmoid Neuron
## Perceptrons and Sigmoid Neuron
The perceptron (or single neuron) is the common ancestor of all deep learning.
The perceptron (or single neuron) is the common ancestor of all deep learning.
A perceptron takes several binary inputs, x1,x2,…, and produces a single binary output:
A perceptron takes several binary inputs, x1,x2,…, and produces a single binary output:
The idea of the perceptron is that it will activate itself based on a composition of its inputs and its internal weights.
The idea of the perceptron is that it will activate itself based on a composition of its inputs and its internal weights.
In fact, each input $x_{j}$ has a corresponding weight $w_{j}$ that will control how relevant the input is for the decision process.
In fact, each input $x_{j}$ has a corresponding weight $w_{j}$ that will control how relevant the input is for the decision process.
The most basic way to do this is to use a sum and threshold:
The most basic way to do this is to use a sum and threshold:
$$
$$
\left\{
\left\{
\begin{array}{l}
\begin{array}{l}
0 \quad if \sum_{j}w_{j}x_{j} \leq threshold\\
0 \quad if \sum_{j}w_{j}x_{j} \leq threshold\\
1 \quad if \sum_{j}w_{j}x_{j} > threshold
1 \quad if \sum_{j}w_{j}x_{j} > threshold
\end{array}
\end{array}
\right.
\right.
$$
$$
By changing the value of each weight, you can change how the decision process will be done.
By changing the value of each weight, you can change how the decision process will be done.
In the context of neural networks, the step function, $if \leq threshold$, is the called an activation function.
In the context of neural networks, the step function, $if \leq threshold$, is the called an activation function.
Now, we will have to do some modification to this perceptron in order for it to be useful.
Now, we will have to do some modification to this perceptron in order for it to be useful.
Indeed, the secret magic sauce of training algorithm of deep learning architecture is the ability to construct models that are fully differentiable in respect to its ouput.
Indeed, the secret magic sauce of training algorithm of deep learning architecture is the ability to construct models that are fully differentiable in respect to its ouput.
However, you can see here that the use of the step function, $if \leq threshold$ is totally not differentiable.
However, you can see here that the use of the step function, $if \leq threshold$ is totally not differentiable.
First of all, let's simplify the use of a threshold by using a bias and recenter the steps function around 0:
First of all, let's simplify the use of a threshold by using a bias and recenter the steps function around 0:
$$
$$
\left\{
\left\{
\begin{array}{l}
\begin{array}{l}
\sigma(x) = \sum_{j}w_{j}x_{j} + b\\
\sigma(x) = \sum_{j}w_{j}x_{j} + b\\
1 \quad if \sum_{j}w_{j}x_{j} + b > 0
1 \quad if \sum_{j}w_{j}x_{j} + b > 0
\end{array}
\end{array}
\right.
\right.
$$
$$
Next, let's change the activation function to the sigmoid function $\sigma(x) = {1 \over {1 + e^{-x}}}$ in order for it to be differentiable:
Next, let's change the activation function to the sigmoid function $\sigma(x) = {1 \over {1 + e^{-x}}}$ in order for it to be differentiable:
$$\sigma(\sum_{j}w_{j}x_{j} + b)$$
$$\sigma(\sum_{j}w_{j}x_{j} + b)$$
This now is not called a perceptron anymore, but a *sigmoid neuron* or *logistic neuron*.
This now is not called a perceptron anymore, but a *sigmoid neuron* or *logistic neuron*.
But enough theory, let's do some practice by implementing this perceptron in tensorflow!
But enough theory, let's do some practice by implementing this perceptron in tensorflow!
%% Cell type:code id: tags:
%% Cell type:code id: tags:
``` python
``` python
# first let's import all that we will need
# first let's import all that we will need
%matplotlibinline
importtensorflowastf
importtensorflowastf
fromitertoolsimportproduct
fromitertoolsimportproduct
importnumpyasnp
importmatplotlib.pyplotasplt
```
```
%% Output
%% Output
/usr/lib/python3.6/site-packages/h5py/__init__.py:36: FutureWarning: Conversion of the second argument of issubdtype from `float` to `np.floating` is deprecated. In future, it will be treated as `np.float64 == np.dtype(float).type`.
/udd/kchoi/igrida/miniconda/envs/gpu/lib/python3.6/site-packages/h5py/__init__.py:36: FutureWarning: Conversion of the second argument of issubdtype from `float` to `np.floating` is deprecated. In future, it will be treated as `np.float64 == np.dtype(float).type`.
from ._conv import register_converters as _register_converters
from ._conv import register_converters as _register_converters
%% Cell type:markdown id: tags:
%% Cell type:markdown id: tags:
Oversimplified, tensorflow is at its core a tensor library with automatic differentiation.
Oversimplified, tensorflow is at its core a tensor library with automatic differentiation.
A *tensor* is a sort of vector, in the mathematical sense, where the important part is to define its size (or shape) and type.
A *tensor* is a sort of vector, in the mathematical sense, where the important part is to define its size (or shape) and type.
One interesting aspect of a tensor is that the data that will flow through this tensor can be fed after the tensor is created.
One interesting aspect of a tensor is that the data that will flow through this tensor can be fed after the tensor is created.
With tensors, you can then do any kind of mathematical operations you want.
With tensors, you can then do any kind of mathematical operations you want.
Every mathematical operations will then produce a new tensor, where it will store its results, that can be then reused to compose with more operations.
Every mathematical operations will then produce a new tensor, where it will store its results, that can be then reused to compose with more operations.
%% Cell type:code id: tags:
%% Cell type:code id: tags:
``` python
``` python
# Let's code a neuron that will do the NAND logical function
# Let's code a neuron that will do the NAND logical function
# This neuron will have two inputs, so a tensor x of size 2
# This neuron will have two inputs, so a tensor x of size 2
defneuron(input_size,weights,bias):
defneuron(input_size,weights,bias):
# tf.placeholder are how we define input tensor. Later, we will be able to fed our data into these tensors
# tf.placeholder are how we define input tensor. Later, we will be able to fed our data into these tensors
x=tf.placeholder(tf.float32,input_size)
x=tf.placeholder(tf.float32,input_size)
# It will also have two weights
# It will also have two weights
w=tf.Variable(weights,dtype=tf.float32)
w=tf.Variable(weights,dtype=tf.float32)
# And a bias
# And a bias
b=tf.Variable(bias,dtype=tf.float32)
b=tf.Variable(bias,dtype=tf.float32)
# we use tf.Variable to notify tensorflow that these tensors are tensors that will be learned during training
# we use tf.Variable to notify tensorflow that these tensors are tensors that will be learned during training
Well, it's not exactly the output we wanted, but that's what you get for manually tuning your weights.
Well, it's not exactly the output we wanted, but that's what you get for manually tuning your weights.
Next, we'll get something out of the way: the batch.
Next, we'll get something out of the way: the batch.
For now, we can only feed one example at a time to our neurone.
For now, we can only feed one example at a time to our neurone.
Keep in mind that transfering data to the gpu is very time consuming, and that you can take advantage of the special architecture of the gpu in order to parallelize the computation of multiple examples.
Keep in mind that transfering data to the gpu is very time consuming, and that you can take advantage of the special architecture of the gpu in order to parallelize the computation of multiple examples.
So by processing examples in batch, we will be faster than computing each example one at a time.
So by processing examples in batch, we will be faster than computing each example one at a time.
%% Cell type:code id: tags:
%% Cell type:code id: tags:
``` python
``` python
# Here, we'll modify our neuron so that it can take a batch of example as input
# Here, we'll modify our neuron so that it can take a batch of example as input
A neuron of $k$ inputs is a small decision unit constituted of:
A neuron of $k$ inputs is a small decision unit constituted of:
* a vector of shape $[k]$ of inputs
* a vector of shape $[k]$ of inputs
* a vector of shape $[k]$ of weights
* a vector of shape $[k]$ of weights
* a bias
* a bias
* an activation function
* an activation function
* if it is the step function, it's a *Perceptron*, it's not trainable
* if it is the step function, it's a *Perceptron*, it's not trainable
* if it is the sigmoid function, it's a *sigmoid* or a *logistic* neuron, and it's *trainable*
* if it is the sigmoid function, it's a *sigmoid* or a *logistic* neuron, and it's *trainable*
* processessing examples in batch is faster
* processessing examples in batch is faster
%% Cell type:markdown id: tags:
%% Cell type:markdown id: tags:
## Multi-Layered Perceptron (MLP)
## Multi-Layered Perceptron (MLP)
To have a more complex model that can do more usefull things, we can stack multiple neurons in parallel in order to make a *layer* of neurons.
To have a more complex model that can do more usefull things, we can stack multiple neurons in parallel in order to make a *layer* of neurons.
Then, when to connect multiple layers one after the other, you obtain what we call a Multi-Layered Perceptrons or MLP.
Then, when to connect multiple layers one after the other, you obtain what we call a Multi-Layered Perceptrons or MLP.
WARNING! Keep in mind that, even though we use Perceptron here, if you want to train this network, you will have to use a Sigmoid neuron or any kind of trainable neuron.
*WARNING*! Keep in mind that, even though we use Perceptron here, if you want to train this network, you will have to use a Sigmoid neuron or any kind of trainable neuron.
Next, let's train this neuron so it will automatically adjust it's weights and bias to compute the NAND function.
As I said earlier, the secret magic sauce of Deep Learning training algorithm is the Gradient Descent algorithm.
The first and mother of all deep learning training algorithm is the gradient descent algorithm.
The Gradient Descent algorithm works on one example at a time.
Instead, the Stochastic Gradient Descent works on a *mini-batch* of examples at a time.
First, we will need a cost function (or loss function or objective function).
The goal of a training algorithm is to tune the weights and biases in order to minimize a *cost function*.
A cost function is a function that tells us how good or bad we are doing.
A cost function is a function that tells us how good or bad we are doing.
You can see the cost function as a distance computation between the output of our neurone and the real value we wanted our network to output.
You can see the cost function as a distance computation between the output of our neurone and the real value we wanted our network to output.
Traditionnally, the quadratic cost function is used in gradient descent tutorial because it's super easy to differentiate:
Traditionnally, the quadratic cost function, also called Mean Squared Error (MSE) is used in gradient descent tutorial because it's super easy to differentiate:
$$
$$
C(w, b) = {1 \over 2} \|real\_output(x) - neurone\_output(x)\|^{2}
C(w, b) = {1 \over 2n} \sum_{x}\|real\_output(x) - network\_output(x)\|^{2}
$$
$$
Here, $w$ denotes the collection of all weights in the network, $b$ all the biases, $n$ is the total number of training inputs, $network\_output(x)$ is the vector of outputs from the network when $x$ is input, and the sum is over all training inputs, $x$.
In order to visualize how gradient descent works, imagine you have two weights: $v_{1}$ and $v_{2}$.
When using the MSE cost function, you can visualize it as a convexe plane where you want to find the minimum of this plane.

Imagine that the current state of your network (with all of its weights and biases) is represented by a point on this plane.
If you can compute the gradient for all weights and biases, you then know in which direction to go in order to find the minimum of this plane.
categorical cross-entropy cost function: Measures the probability error in discrete classification tasks in which the classes are mutually exclusive (each entry is in exactly one class).
### using MLP
The code comes entirely from this keras examples: https://github.com/keras-team/keras/blob/master/examples/mnist_mlp.py