diff --git a/1. Introduction to Deep Learning.ipynb b/1. Introduction to Deep Learning.ipynb
index 8cd156e4d5e2f97bb7a825ad5b6dffde0154dac9..9f8f5a6486c758b58846ab6d0e4592560d16876d 100644
--- a/1. Introduction to Deep Learning.ipynb
+++ b/1. Introduction to Deep Learning.ipynb
@@ -70,15 +70,18 @@
"name": "stderr",
"output_type": "stream",
"text": [
- "/usr/lib/python3.6/site-packages/h5py/__init__.py:36: FutureWarning: Conversion of the second argument of issubdtype from `float` to `np.floating` is deprecated. In future, it will be treated as `np.float64 == np.dtype(float).type`.\n",
+ "/udd/kchoi/igrida/miniconda/envs/gpu/lib/python3.6/site-packages/h5py/__init__.py:36: FutureWarning: Conversion of the second argument of issubdtype from `float` to `np.floating` is deprecated. In future, it will be treated as `np.float64 == np.dtype(float).type`.\n",
" from ._conv import register_converters as _register_converters\n"
]
}
],
"source": [
"# first let's import all that we will need\n",
+ "%matplotlib inline\n",
"import tensorflow as tf\n",
- "from itertools import product"
+ "from itertools import product\n",
+ "import numpy as np\n",
+ "import matplotlib.pyplot as plt"
]
},
{
@@ -138,7 +141,7 @@
},
{
"cell_type": "code",
- "execution_count": 28,
+ "execution_count": 3,
"metadata": {},
"outputs": [],
"source": [
@@ -158,7 +161,7 @@
},
{
"cell_type": "code",
- "execution_count": 5,
+ "execution_count": 4,
"metadata": {},
"outputs": [
{
@@ -195,7 +198,7 @@
},
{
"cell_type": "code",
- "execution_count": 34,
+ "execution_count": 5,
"metadata": {},
"outputs": [],
"source": [
@@ -225,7 +228,7 @@
},
{
"cell_type": "code",
- "execution_count": 35,
+ "execution_count": 6,
"metadata": {},
"outputs": [
{
@@ -234,7 +237,7 @@
"array([0.95257413, 0.7310586 , 0.7310586 , 0.26894143], dtype=float32)"
]
},
- "execution_count": 35,
+ "execution_count": 6,
"metadata": {},
"output_type": "execute_result"
}
@@ -269,106 +272,600 @@
"\n",
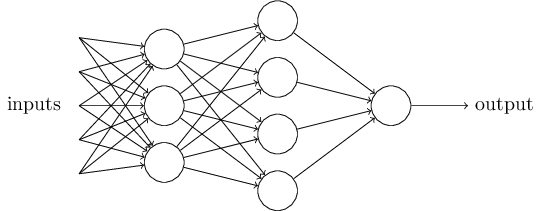
"To have a more complex model that can do more usefull things, we can stack multiple neurons in parallel in order to make a *layer* of neurons.\n",
"Then, when to connect multiple layers one after the other, you obtain what we call a Multi-Layered Perceptrons or MLP.\n",
- "WARNING! Keep in mind that, even though we use Perceptron here, if you want to train this network, you will have to use a Sigmoid neuron or any kind of trainable neuron.\n",
"\n",
- "\n",
- "\n"
+ "*WARNING*! Keep in mind that, even though we use Perceptron here, if you want to train this network, you will have to use a Sigmoid neuron or any kind of trainable neuron.\n",
+ "\n",
+ "\n",
+ "\n",
+ "Let's implement an MLP in ternsorflow!"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 75,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "network_output: Tensor(\"Add_33:0\", shape=(?, 1), dtype=float32)\n",
+ "network layers: [<tf.Tensor 'Placeholder_37:0' shape=(?, 3) dtype=float32>, <tf.Tensor 'Sigmoid_30:0' shape=(?, 4) dtype=float32>, <tf.Tensor 'Add_33:0' shape=(?, 1) dtype=float32>]\n",
+ "network weights and biases: [[<tf.Variable 'Variable_74:0' shape=(3, 4) dtype=float32_ref>, <tf.Variable 'Variable_75:0' shape=(4,) dtype=float32_ref>], [<tf.Variable 'Variable_76:0' shape=(4, 1) dtype=float32_ref>, <tf.Variable 'Variable_77:0' shape=(1,) dtype=float32_ref>]]\n"
+ ]
+ }
+ ],
+ "source": [
+ "def build_neuron_layer(input_tensor, num_neuron, last_layer=False):\n",
+ " \"\"\"\n",
+ " input_tensor: tensor with shape [batch_size, input_size]\n",
+ " num_neuron: number of neurons in the layer, also the output_size\n",
+ " Here, we will use a random distribution in order to initialize weights and biases\n",
+ " \"\"\"\n",
+ " # you now have number of inputs * number of neurons weights\n",
+ " weights = tf.Variable(tf.random_normal(tf.TensorShape([input_tensor.shape[1], num_neuron])))\n",
+ " # you have one bias per neurons\n",
+ " biases = tf.Variable(tf.random_normal([num_neuron]))\n",
+ " # you can do the weighted sum using a matrix multiplication\n",
+ " weighted_sum = tf.matmul(input_tensor, weights)\n",
+ " # then add biases\n",
+ " add_biases = tf.add(weighted_sum, biases)\n",
+ " # apply the activation function\n",
+ " if not last_layer:\n",
+ " layer_output = tf.sigmoid(add_biases)\n",
+ " else:\n",
+ " layer_output = add_biases\n",
+ " return layer_output, [weights, biases]\n",
+ "\n",
+ "def build_mlp(batch_size, input_size, layer_shapes):\n",
+ " \"\"\"\n",
+ " batch_size: size of the batch, can be None for variable batch size\n",
+ " input_size: input size of the placeholder input tensor\n",
+ " layer_shapes: list of int, for example [2, 3, 1]\n",
+ " Here there are 3 layers (2 hidden layers and 1 output layer) of respective shape 2, 3, and 1\n",
+ " \"\"\"\n",
+ " x = tf.placeholder(tf.float32, [batch_size, input_size])\n",
+ " layers = [x]\n",
+ " variables = []\n",
+ " for i, size in enumerate(layer_shapes):\n",
+ " is_last_layer = i == (len(layer_shapes) - 1)\n",
+ " layer, variable = build_neuron_layer(layers[-1], size, is_last_layer)\n",
+ " layers.append(layer)\n",
+ " variables.append(variable)\n",
+ " return layers[-1], layers, variables\n",
+ "\n",
+ "network_output, layers, variables = build_mlp(None, 3, [4, 1])\n",
+ "print(\"network_output:\", network_output)\n",
+ "print(\"network layers:\", layers)\n",
+ "print(\"network weights and biases:\", variables)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
+ "## (Stochastic) Gradient Descent\n",
"\n",
- "Next, let's train this neuron so it will automatically adjust it's weights and bias to compute the NAND function.\n",
- "The first and mother of all deep learning training algorithm is the gradient descent algorithm.\n",
+ "As I said earlier, the secret magic sauce of Deep Learning training algorithm is the Gradient Descent algorithm.\n",
+ "The Gradient Descent algorithm works on one example at a time.\n",
+ "Instead, the Stochastic Gradient Descent works on a *mini-batch* of examples at a time.\n",
"\n",
- "First, we will need a cost function (or loss function or objective function).\n",
+ "The goal of a training algorithm is to tune the weights and biases in order to minimize a *cost function*.\n",
"A cost function is a function that tells us how good or bad we are doing.\n",
"You can see the cost function as a distance computation between the output of our neurone and the real value we wanted our network to output.\n",
- "Traditionnally, the quadratic cost function is used in gradient descent tutorial because it's super easy to differentiate:\n",
+ "Traditionnally, the quadratic cost function, also called Mean Squared Error (MSE) is used in gradient descent tutorial because it's super easy to differentiate:\n",
"\n",
"$$\n",
- "C(w, b) = {1 \\over 2} \\|real\\_output(x) - neurone\\_output(x)\\|^{2}\n",
- "$$"
+ "C(w, b) = {1 \\over 2n} \\sum_{x}\\|real\\_output(x) - network\\_output(x)\\|^{2}\n",
+ "$$\n",
+ "\n",
+ "Here, $w$ denotes the collection of all weights in the network, $b$ all the biases, $n$ is the total number of training inputs, $network\\_output(x)$ is the vector of outputs from the network when $x$ is input, and the sum is over all training inputs, $x$.\n",
+ "\n",
+ "In order to visualize how gradient descent works, imagine you have two weights: $v_{1}$ and $v_{2}$.\n",
+ "When using the MSE cost function, you can visualize it as a convexe plane where you want to find the minimum of this plane.\n",
+ "\n",
+ "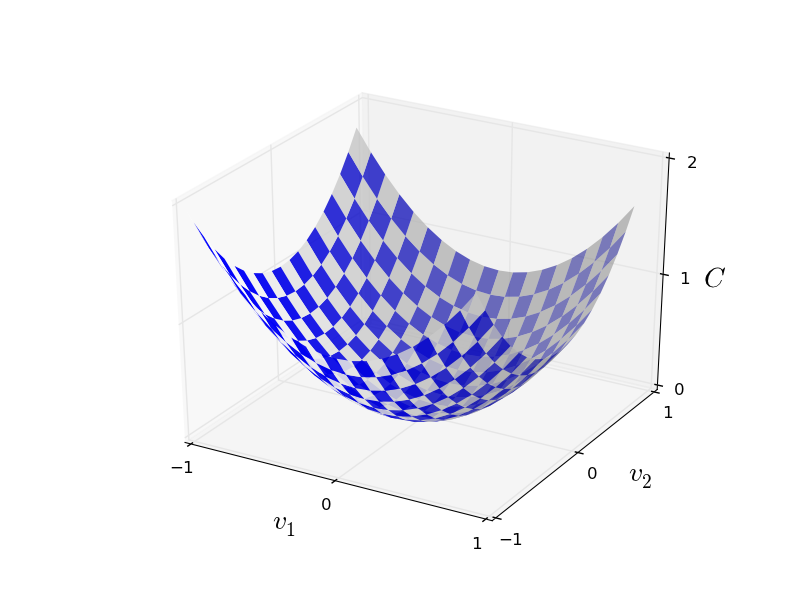\n",
+ "\n",
+ "Imagine that the current state of your network (with all of its weights and biases) is represented by a point on this plane.\n",
+ "If you can compute the gradient for all weights and biases, you then know in which direction to go in order to find the minimum of this plane.\n",
+ "\n",
+ "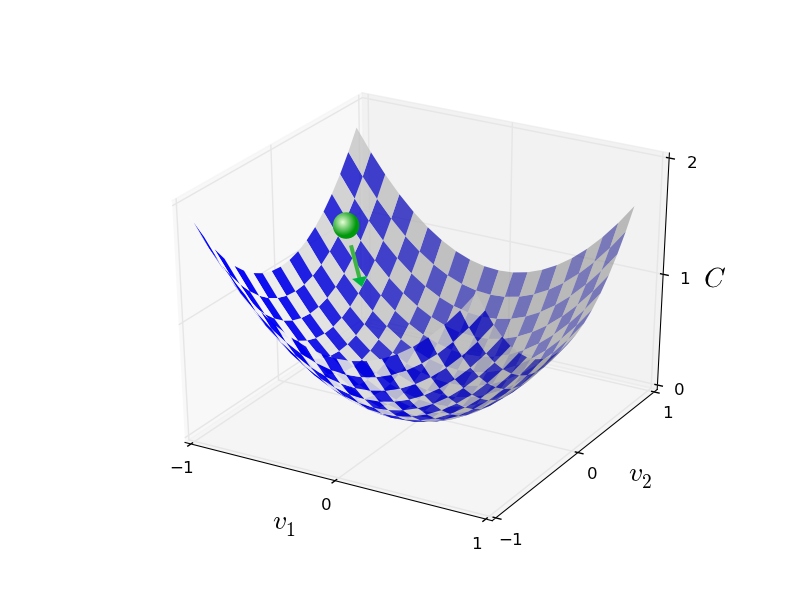\n",
+ "\n",
+ "You just need to substract the gradients to your weights and biases and you will obtain and slightly better model than before.\n",
+ "One important parameter here is called the *learning rate*.\n",
+ "The *learning rate* is a number by which we will multiply the gradients before applying them to the weights.\n",
+ "Having a big *learning rate* means that you will learn faster, but you have a risk of missing the minimum point and \"going to far\".\n",
+ "Having a small *learning rate* means that you will learn slower, but you are \"quite\" sure that you won't miss the minimum point."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
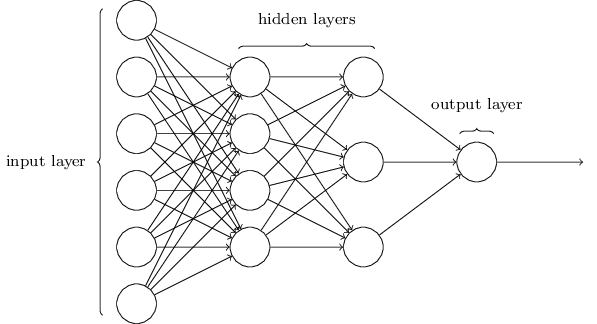
+ "# Training for Regression\n",
+ "\n",
+ "Let's train a neural network to approximate a function like $cos$.\n",
+ "Neural Networks are known to be *Universal Approximator*.\n",
+ "This means that with a network of only 1 hidden layer, you can approximate *any* function you want.\n",
+ "The only matter is that we don't know how many neurons in that layer is needed to approximate a given function.\n",
+ "It's a matter of experimentation to find the correct number of neurons in order to produce the precision you want, with the complexity you want."
]
},
{
"cell_type": "code",
- "execution_count": 6,
+ "execution_count": 87,
"metadata": {},
"outputs": [],
"source": [
- "real_output = tf.placeholder(tf.float32, )"
+ "def build_model_regression(batch_size, input_size, hidden_layer_size, output_size, learning_rate):\n",
+ " network_output, layers, variables = build_mlp(batch_size, input_size, [hidden_layer_size, output_size])\n",
+ "\n",
+ " real_cos = tf.placeholder(tf.float32, [batch_size, input_size])\n",
+ " cost = tf.losses.mean_squared_error(real_cos, network_output)\n",
+ " train_ops = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost)\n",
+ " return network_output, layers[0], real_cos, cost, train_ops"
]
},
{
"cell_type": "code",
- "execution_count": 30,
+ "execution_count": 88,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
- "array([[ 0, 0],\n",
- " [ 0, -2],\n",
- " [-2, 0],\n",
- " [-2, -2]])"
+ "(array([[0.14152461],\n",
+ " [2.46041363],\n",
+ " [2.44419513],\n",
+ " [4.25312064]]), array([[ 0.9900021 ],\n",
+ " [-0.77683082],\n",
+ " [-0.76651616],\n",
+ " [-0.44329238]]))"
]
},
- "execution_count": 30,
+ "execution_count": 88,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
- "import numpy as np\n",
- "a = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])\n",
- "b = np.array([-2, -2])\n",
- "a * b"
+ "def get_cos_batch(batch_size, cos_range=[0, 2 * np.pi]):\n",
+ " x = (np.random.rand(batch_size) * (cos_range[1] - cos_range[0])) + cos_range[0]\n",
+ " # reshape as how the network is asking the input to be\n",
+ " x = x.reshape([batch_size, 1])\n",
+ " return x, np.cos(x)\n",
+ "get_cos_batch(4)"
]
},
{
"cell_type": "code",
- "execution_count": 26,
+ "execution_count": 116,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "# Let's do our training loop!\n",
+ "def train_regression(batch_size, input_size, hidden_layer_size, output_size, learning_rate,\n",
+ " num_steps, print_frequency=10):\n",
+ " network_output, network_input, real_cos, cost, train_ops = build_model_regression(\n",
+ " None, input_size, hidden_layer_size, output_size, learning_rate\n",
+ " )\n",
+ " x = np.linspace(0, 2 * np.pi, 200)\n",
+ " plt.plot(x, np.cos(x), linewidth=2)\n",
+ " init = tf.global_variables_initializer()\n",
+ " sess.run(init)\n",
+ " for i in range(num_steps):\n",
+ " batch_x, batch_real_cos = get_cos_batch(batch_size)\n",
+ " sess.run(train_ops, feed_dict={network_input: batch_x, real_cos: batch_real_cos})\n",
+ " if i % (num_steps // print_frequency) == 0:\n",
+ " print(\"step:\", i, \"loss:\", sess.run(cost, feed_dict={network_input: batch_x, real_cos: batch_real_cos}))\n",
+ " plt.plot(\n",
+ " x, \n",
+ " sess.run(network_output, feed_dict={network_input: np.expand_dims(x, axis=1)}),\n",
+ " '--',\n",
+ " linewidth=1,\n",
+ " label=\"step {}\".format(i))\n",
+ " plt.plot(x, sess.run(network_output, feed_dict={network_input: np.expand_dims(x, axis=1)}),\n",
+ " linewidth=2)\n",
+ " plt.title(\"Comparison between real cos and our trained model\")\n",
+ " plt.show()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 139,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
- "Tensor(\"Placeholder_8:0\", shape=(4, 2), dtype=float32) <tf.Variable 'Variable_8:0' shape=(2,) dtype=float32_ref> Tensor(\"mul_11:0\", shape=(4, 2), dtype=float32)\n"
+ "step: 0 loss: 1.0012071\n",
+ "step: 200 loss: 0.3319829\n",
+ "step: 400 loss: 0.16274151\n",
+ "step: 600 loss: 0.17327055\n",
+ "step: 800 loss: 0.053479217\n"
]
+ },
+ {
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAX8AAAEICAYAAAC3Y/QeAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAAIABJREFUeJzsnXd4FcX6xz9zSnrv9BBa6FU6osiVLqigIKB4f4KoVxC7XAXFjnhBxWvvvaGgIBcB6TX0GkoSkpDek5Ny2vz+2AOckEJLgWQ+z8NDdqfsu7sz350z5R0hpUShUCgU9QtdbRugUCgUippHib9CoVDUQ5T4KxQKRT1Eib9CoVDUQ5T4KxQKRT1Eib9CoVDUQ5T41yJCiIlCiFU1fM04IcTgmrzmtYoQIlwIIYUQhtq25UoRQjwvhPi6tu24XIQQA4QQ0dWU9+dCiJeqI+8LXPeiy5cQYooQYlNVXr9OiL8Q4i4hRJQQokAIkSyE+FMI0b+27boQUspvpJQ317YdF4v6cCguh6r48EgpN0op21SVTYo6IP5CiEeBRcArQCjQFPgvMLo27boQdaE1ebWjnnHNcznPXGhc81p0zSGlvGb/Ab5AATCukjiuaB+HJMe/RYCrI+wGIBF4EkgDkoExwHDgGJAFzHbK63ngZ+AHIB/YDXR2Cn8aOOkIOwzc6hQ2BdgMLHTk+5Lj3CZHuHCEpQG5wH6gg9N9fgmkA6eAZwGdU76bgAVANhALDKvkecQBzzjsywY+A9ycwkcCe4EcYAvQyXH+K8AOFDme+ZPAF8BjjvBGgAQedBy3dNynqCxfR1hD4BfH/cUCM8575j867j8fOAT0qOT+JPAQcByIdZyLBP5y2BMN3OEUfwSwB8gDEoDnncLCHfkZKrhWE2CJw+5MYLHjvM7xjk453ueXgK8jzA342hE/B9gJhFaQ/4XKU4XvHWgOrHek/QtYDHxdyXObCpxwPKNlQMOKngGwDrivonJ9Xr5DATNgcZSbfU55vOxIW+QoL/cCRxw2xwD3O+VzA5B4Xjl+HK2e5KLVyQuWY0dYV7S6m+9I9/35dldQb3McdvV1nE9wvN97ztOkiuqq3vG+Mhz5POT8bB1pP0HTodNoGqF3ft9Vqp9VmVlN/3MULCsVVE5HnHnANiAECHYUhBedCpQVmAMYHRUgHfgW8AbaA8VAhCP+845CPNYR/3G0Smd0hI9DEzIdcCdgAho4vTwr8DBgANwpLf5DgF2AH9qHoK1T2i+BpQ6bwtE+TP/nlK/FYbseeADtIycqeB5xwEE04QpwFOyXHGHdHIW5lyOvexzxXZ3SDnbK65/A746/70ITqh+cwpZeKF/Hs9rleAcuQARaxRji9MyL0T7IeuBVYFsl71uiiV2A4xl7olXSex3PvRta5WvvVAY6OuzoBKQCYyoSPqfr6IF9aKLgiSbq/Z3u/YTjXrzQPhBfOcLuB34HPBx5dAd8KriXC5WnCt87sBX4j+MZX48mdOWKPzDI8Uy6OeK/A2yo6BlQVvxLlety8n/+/Gs78ohHq2MGtPo0AmiBVv4HAoVAN6f3dL7473A8nwC0j8b0iyhvLmiiPMtxzbGO51iZ+FvRyo8eTZDjgXcd+d3seLZeF1FXpwNHOVf3/qa0+P8GfIBWnkIc93e/kx1K/J1ezEQg5QJxTgLDnY6HAHFOBaqIc19Xb8fL6OUUfxfnxOB5nIQHrVImAwMquPZeYLTTy4svp2CdEf9BjoLSG0dLwXFeD5QA7ZzO3Q+sc8rjhFOYh+MewiqwKe5MJXEcDwdOOv5+D8eH0Sk8GhjolNZZ/FugtYZ0wPsOuxIdYV8Aj14oX7QKev5zeQb4zOmZr3YKawcUVfK+JTDI6fhOYON5cT4A5laQfhGw0PF3OBWLfx+0hkJ5YWtw/AJyHLdBExgD2oehVEv0Esr7+eWp3PeO1vVpBTydwr+lYvH/BJjvdOzlsDe8vGdAWfGPv4Ddz59/bUce8y6Q7jdgplNdPV/8Jzkdzwfev4jydj3nNY4c76My8T/udNzR8TxCnc5lAl24cF1dS+m6d/OZZ4vWZV2C08cTmAD87WRHlYr/td7PlgkEXaCfsSHal/4MpxznzuYhpbQ5/i5y/J/qFF6EVhnOkHDmDymlHa3bqCGAEOJuIcReIUSOECIH6AAElZf2fKSUa9F+mr8LpAohPhRC+DjSn2mtON9DI6fjFKd8Ch1/Ott8Ps52OD+PZsBjZ+x33EMTSj8vZ5tPov2U7wIMAP4AkoQQbdAq2vqLyLcZ0PC8sNlolaHM/aG1Bt0u8M6d768Z0Ou8/CeiiSRCiF5CiL+FEOlCiFy01llQ2SzL0AQ4JaW0lhNWXpk7U8G/Av4HfC+ESBJCzBdCGMu7wEWUp4ree0MgW0ppOs+Giihlr5SyAK1uNaowRWkqLNeXkk4IMUwIsU0IkeW43+FU/i7OLxdnynxl5a0hcFo6FNVBZc8GyuoBUsryNOJCdbUhZeveGZqh/RJJdrL5A7RfANXCtS7+W9G6BMZUEicJ7cGeoanj3OXS5MwfjkGqxmiC1wz4CPgXECil9EPrXhFOaZ0LXBmklG9LKbuj/RRuDTyB9nPcUs49nK6Ke6D080gAXpZS+jn985BSfleJ/evRfjq7SClPO47vBvzRWqoXyjcBrW/eOcxbSjn8Cu7P2c4EYP15+XtJKR9whH+L1sfdRErpi/YLRnBhEoCmFXyEyitzViBVSmmRUr4gpWyH1nc8Eu15leIiy1NFJAP+QgjP82yoiFL2OtIFopWxMx8QD6f4Yeelr7RcVxJ+9rwQwhVt3GcBWqvaD1jBxd3v+VRW3pKBRkII53wrezaXwoXqajJl656zzSVAkJPNPlLK9lVkWxmuafGXUuai9RW/K4QYI4TwEEIYHS2I+Y5o3wHPCiGChRBBjvhXMu2suxDiNkelfwTthW1D66eTaF0BCCHuRWupXRRCiOscrVAjWoUrBmyOXyU/Ai8LIbwdovDoFd7DQ0KIxkKIALRW9g+O8x8B0x12CCGEpxBihBDC2xGeitaP7cx6NIHa4Dheh9b/u8npF1Vl+e4A8oQQTwkh3IUQeiFEByHEdVdwf878AbQWQkx2lA2j41m3dYR7A1lSymIhRE+0sYuLYQdaZX7NcT9uQoh+jrDvgFlCiOZCCC+0mWg/SCmtQogbhRAdhRB6tEFmC2ArJ//LLk9SylNAFPCCEMLFMe15VCVJvgXuFUJ0cYjwK8B2KWWclDIdTbwmOd7NP9G6+y6FVCD8AjN6XND60NMBqxBiGFq3yOVQWXnbivYhniGEMAghbgN6XuZ1SnERdfVHx3UbCyH80Qb0z6RNBlYBbwohfIQQOiFECyHEwKqwrTyuafEHkFL+B+0BP4tWcBLQxOg3R5SX0CrCfuAA2ij/lSzoWIrWj5wNTAZuc7TmDgNvohWuVLS+wc2XkK8PWqHNRvs5mInWCgJNTE1oA6Gb0Crrp1dwD9+iFbQYx7+XAKSUUWgDiIsddpxA62s8w6toH9IcIcTjjnPr0QT0jPhvQmslnjmuNF9HhRmF1nUUi9Z6+hht5sMVI6XMRxOR8Wgt3BTgdTShAXgQmCeEyEdrGPx4kfmesbsl2gBgIlq5AO3dfIX2DGLRPuQPO8LC0GaM5aENUq6nnA95FZSnu9DGU7KAuWgDkRXdyxrgObSWdzKauI93ijIV7VdoJtqv0i2XYAfAT47/M4UQuyuwIR+Ygfb8sx32L7vE65zJq7LyZgZucxxno72zJZdznQqorK5+hNbltw9Nh86/7t1oH8EzM/F+BhpUoW2lODMzQHERCCGeB1pKKSfVti0KhUJxJVzzLX+FQqFQXDpK/BUKhaIeorp9FAqFoh5SJS1/IcSnQog0IcTBCsJvEELkOuYs7xVCzKmK6yoUCoXi8qgqx1efo42sVzijAG2V5ciLzTAoKEiGh4dfoVkKhUJRv9i1a1eGlDL4QvGqRPyllBuEEOFVkdcZwsPDiYqKqsosFQqFos4jhLjQimWgZgd8+wgh9gnN1365q9aEENOE5pc/Kj09vQZNUygUivpFTYn/bqCZlLIzmsfA38qLJKX8UErZQ0rZIzj4gr9aFAqFQnGZ1Ij4SynzHM6ikFKuAIwOVwsKhUKhqAVqRPyFEGFnHCk5/Kfo0JaKKxQKhaIWqJIBXyHEd2j+toOEEIlovkSMAFLK99G8Pj4ghLCiuT8dL9UCA4VCoag1qmq2z4QLhC9GmwqqUCgUiqsA5d5BoVAo6iF1VvxVr5JCoVBUTJ0U/93/O8WeVfG1bYZCoVBctdRJ8W/ZI4S9q+NJO5VX26YoFArFVUmdFH+fQHcG3NGavz49jKWkvB3yFAqFon5TVY7drjpaXReK3qhDb6yT3zeFQqG4Iuq0MkZ0CSbpeA6nDqr1ZAqFQuFMnRZ/AL1Bx5ovj2DKLaltUxQKheKqoU6Kf2FeLqacbAAatPClw4CGrP3iiJr+qVAoFA7qpPgf2biO3954EYtZa+33GB6Ou48LxSZLLVumUCgUVwd1Uvy7Db8Fv9AGrPzvIqTdjk6vY/CUdugNOgrzzLVtnkKhUNQ6dVL8hRAMmT6Twtxs0uJizp4/sjmZNV8cVt0/CoWi3lMnxd+cVIDeYOSO514hNKIlOakpAHS4oRGFeWaObk2uZQsVCoWidqlz4l90NIu0d/eS89sJQFCYm8O3zz7G6aOH0et13HRPO7b9FoO52FrbpioUCkWtUefEX+gFCIFpRwo5v53A3duXYQ89yu8LXyU/M4Ogxl7c8e/rcHGrs+vbFAqF4oLUOfF3a+WPZxcL6Dn7AQjv1I2uQ0exc9kvAHj6unJgXSLR21Nq2VqFQqGoHepk81fvVYL5+FJcWt+FaYcm8NfdcjsSibmoEBd3D0Kb+/DHu/tp2j4Ady+XWrZYoVAoapY61/IH8B5yM8YQHQafY2DQYdqRQu7SGHQ6PUsXvMSh9WsIaeZD6x6hbPnlRG2bq1AoFDVOnRR/IQRhz83BcnIHgXdHah+AnSnkLo/hhrunsv6rT0iNPUnPW5rj5e+GtKupnwqFon5RJ8UfwBgaQpMP3selgQuBk9qAXlCwOQnXk3oG/XM6fy5+E4OLoNctEWQmmbBZ7LVtskKhUNQYdVb8z5DywjwKNy8jYHwbEJC36hSNda0Y++8X0en0SCnZuTyWXf87VdumKhQKRY1R58U/eMbDZH70EQafQvzGtAQgZ+kJdIl2diz9mb2rltN/XCsOrEskO8VUy9YqFApFzVDnxd+laVMCp00j5YV5ePVqgM+QcJCQ9UM0zUM7s/WnbynKS6LH8HB2/BFb2+YqFApFjSCuVj83PXr0kFFRUVWSl7RaMcfG4tqqFVJKcpfHUrDpNMJFT37PYrau+ZG7Xl6I0BnV4i+FQnFNI4TYJaXscaF4db7lDyAMBlxatiTtzf9gz8vDd3hz3DsHI802fA940e+WiRhdXdDpBSve269cPygUijpPvRB/0KZ/2grySVu4EKETBIxtjUszH2y5Jfge8iLpSDRxe3fi6m4ganlcbZurUCgU1Uq9EX+AkFmzKFizlqK9exFGHYGT26IPcMOSWIDYVMCqD9+hw0BfjmxNVoO/CoWiTlOvxF/v40PI009RdPCQduzlQtCU9gg3PTKuhBs7TGLD1/+l720RatMXhUJRp6lX4g/gO2IEAZMmYsvJAcAY4kHgpLagE3gne9HEpQ1N23nQoKUfuemFtWytQqFQVA/1TvwBrNnZnBwxEkuK5vTNraU/fmNaANA4PwKRbSduXxy/LdyDxWyrTVMVCoWiWqiX4m/w98fvjnGkzX/j7Dmvng3w7BUGVknGF4eI+ukDwsK92L1SrfxVKBR1jyoRfyHEp0KINCHEwQrChRDibSHECSHEfiFEt6q47pUQNG0ahXv2ULhz59lzfqNa4NLUG12xoL3og5v7AQ6uP636/xUKRZ2jqlr+nwNDKwkfBrRy/JsGvFdF171sdO7uNHn/Pdzatz97Thh0BE5qi87biK8tAHblMmx6BO7exlq0VKFQKKqeKlnOKqXcIIQIryTKaOBLqS0n3iaE8BNCNJBSVvlO6nEZJlYfScXL1YCXmwEvVwON/d1pFuiJUV/6W+fWpg3FR49iPhWPz5CbAdD7uBI4sS3pHx6ghVsn/ExGjm5Nwb+BB2HNfavaXIVCUc8pKLFyMq2A9PwSTGYr+cVWCs1Wpl3folqvW1O+DBoBCU7HiY5zVS7+h5LyeGn5kTLnDTpBs0APujTxp3+rQPq1CCLExw2EjpQXXsCj53UY/P0BcA33xW9UBDlLT5L541FOB8ZzyBrJ7U92RwhR1SYrFIp6gpSS6NR8Nh3PYMvJTI4k55GcW1xu3Hv6huNq0FebLTUl/uUpZhmnQkKIaWjdQjRt2vSyLtQs0IN7+4VjKrFSUGIlt8jCqcxCErOLOJlu4mS6iV92JwLQqbEvt3VtxA3/GEL6ordo8MLzZ/Px7N0Ac3w+hXvSaJjsTbp7Gsd3ptK6Z9hl2aVQKOovx1Pz+Xl3Ikv3JJGSV1rsXfQ6mgd50sDPDW83o9Zr4arHXs1bjNSU+CcCTZyOGwNJ50eSUn4IfAiaY7fLuVCHRr50aFS2e6bIbONEWgHbYzPZdCKD7TFZ7E/MZX9iLn62dizc/QWZJ1Pp0CIU0NxB+I1piTkxH5/0ACJKYkk+ka3EX6FQXBQ2u2TlwRQ+3BjDvoScs+dDfVzp1yKIfi2D6NbMnyb+7hj0NT/xssq8ejr6/P+QUnYoJ2wE8C9gONALeFtK2bOy/KrSq2d5FFts/HU4lV92J7LhWDp2u0Qn7fRvE8qMm1rRIzwAAHOyibR394LVjs/YCDw7N0BvrJczZBUKxUVgtdlZsvs0760/SWyG5ibG283AyE4Nub1bI7o386/W7uOL9epZJeIvhPgOuAEIAlKBuYARQEr5vtDudDHajKBC4F4pZaXKXt3i70xybhGfbIwl8J1X2RHUir+bdGdExwY8PSySJgEeFGxPJufXE2AUbC4uYOS/b8TTz7VGbFMoFNcOm45n8OIfh4lOzQegSYA791/fgrHdG+NmrL7+e2dqVPyrg5oU/zOkbosiaeZM7r3xcXJwwcWgY/r1ETx4YwtMPx2naH8GefYckttGcNO97S+coUKhqBck5RQxd9kh/jqcCkBjf3cev7kNIzs1qPEuHeXP/zII7d2D0BuvZ4nPcUZ3aYjZaufttScYvXgLyX1C0Qe44qPzw2X/cdLj82vbXIVCUctIKfkxKoEhCzfw1+FUPF30PDGkDasfHciYro1qpS//YqmTLf/orGiEELT2b33JaS2paZQci8ZrwAB2xGbx5M/7iMssRK8TPNu9Gf+IygIJHuNaEdBdDf4qFPWV9PwSnvx5H39HpwMwuG0oL9/agVAft1q1q163/GNyY3h4zcNkFGVcclpjaAievXqRv/ZvejYPYMXMAUzpG47NLnlhZxx/+muPrGhFHGnHsqvadIVCcQ2wMy6Lke9s5O/odHzcDCy8szMf3d291oX/UqiT4j+s+TDGtBzDzLUzKbaWv4CiMqTNRsqLL1K4ezceLgaev6U9397XiyAvF17NyuGw3o40WUj4NAqbrZon4yoUiqsGKSUfb4xh/IfbSM0roWd4AKtmDeTWro2vuQWgdVL8AaZ3nk6HoA6cLjh9yWl17u6EzHqE1FdeRTpWWvRtGcTyGQPoHu7PXJuJImkjFDdO/hRd1aYrFIqrkBKrjcd+3MdLy49gs0umXR/BN1N7EeZ77bT2namz4i+E4Jlez9DMpxkbEzdecnqfkSNBp6Nwxzmvn6E+bnw7tTfD+oXzH0oAMO5JxZyhNn1RKOoyOYVm7v5kB0v2nMbDRc/7k7oxe3jbMv7CriWuXcsvknxzPi9vf5k/Yv64pHRCp6PZ55/h2btXqfNGvY45o9rRd0wbttgLMQo9u9/bQ4na9EWhqJMkZBVy23tb2B6bRYi3Kz/e34ehHRrUtllXTJ0Xf383f94Z9A5v7HyDvWl7LymtzsOD/NWryfzk0zJhk/uEEzqxI1nYaWyy89Wi7RRb1AdAoahLnEgrYNz7W4lJNxEZ5s1vD/Ur133MtUidF3+AVv6teLHfi2xI3HDJaV0j25L54YdYUlPLhA3s3BDDMM0B3U2ZFh7/cDsFJdYrtlehUNQ+h5JyufODraTkFdOzeQA/Te9DQz/32jaryqgX4g9wfePrmdFtBkcyj5BvvvgFWi6NG+F3xx2kL1xUbni7gc3JDbZhFDpGxZcw+aNt5BVbqspshUJRC+xLyGHCh9vINJm5vnUwX9zbE2+3urWpU70R/zMsO7mMJzY8gc1+8V00gfdPQ+fhcXbmz/lEPtCPYllMe2GgZWIR9362E5P6BaBQXJMcPJ3L5E+2k1dsZUj7UD66uzvuLjXjl6cmqXfi/1iPx7DarSzctfCi0+i9vAib8xzW9HTKWxGt9zASOkFzZjodV1JO5fB/X+ykSA0CKxTXFMdS80sJ/+K7ulXrhiq1Sb0Tf4POwJsD3+RQ5iFyS3IvKW3iwzPIX/VXuWHeXRpQGASuCOboPdkek8W0r6IosaoPgEJxLRCbYeKuj7aTXWjhxjbBvDOhW61M5bSkFVJ44NK9E1wq9U78AXxdffls6Gd4GDw4lXfqotOFPDKTtAULsJvN5YY3nNyRYlsh7W06Jrm4s/F4Bo/9uA+7/er0n6RQKDTS8oqZ/Ml2MgpK6NsikPcmdcfFULPyKC12clfFkfrWbrJ/jMaac+neCS6Fein+Z9iXvo9/rvwnqaayM3nKw7NvX1xbtCD7m2/LDfcK9SOrmdbXP83uSnMXI3/sT+aVFWX3FFYoFFcH+cUWpny2k8TsIjo38ePje3rUmO/9MxSfyCb1rd3kr00Am8S9czCimm2o1+LfI6wHE9pOYObfF+8DKGzOc/jeMqriPB8cRrZrLsJq54PQYIw6wcebYvl4Y0xVma1QKKoIs9XOA1/v5nByHs2DPPn0nh54uNTU7rZgKzCT9UM0GR8fxJpRhCHEneD7OxEwtjV6z+qdXVSvxR/g/zr8H019mrI6fvVFxTc2bIg0m8n+6adyw3U6HW0f/QfSIPBIKODjPi0AeGn5EVYcSK4yuxUKxZUhpWT2rwfYdCKDIC8Xvri3J4FeNbNDn5SSwn1ppC7cReGeNDDo8BnSjNAZ3XBtXjOLyOq9+AsheLX/q4yMGHnRLqCFqyvpb/6HkpjYcsMNvq4cLjoGQKv92Tw3WNtX4LEf93Eo6dIGmRUKRfXw8cZYft6ViLtRz2dTetI00KNGrmvLM5P51RGyvovGbrLi2tKPsFnd8LmxKaIGxxnqvfgD6HV6LDYLk1ZMYn3C+gvGNwQEEDj1PtIWLKgwTvupQ0gvTsKeb+HWPBjbvTFFFhtTv4giPb+kKs1XKBSXyN/Rabz6pzYW9587OtOxcfW3tqWUmHalkvKfXRQfzkS46vG/rRVB/9cBQ2DNrxxW4u/AqDfy+vWvM2fLHE7mnLxgfP9Jk7CmpWFNTy83vHFkI+K9C7Fjp3BHCs93bUq3pn4k5RYz/etdagqoQlFLnEgrYMa3e7BLeGRwK4Z1rH4nbdbcEjI/P0T2T8eQxVbc2vgTOqs7nj3Dam0fACX+TnQO7syj3R/ltR2vXTCuztWV8J9+RB8UVO7CL4AhT0/ArVcQAAXLTvLehK408HVj16lsnv31YIXpFApF9ZBbaGHql1Hkl1gZ3jGMGYNaVfs1tb793RRHZyPcDPiPa03glPYY/MofX8hJTal2m0CJfxlGtxzN24PexmwzY7VX7qJBCEHaa6+T+9vScsPdPN0oaRlAkSjGmlaE+54MPrq7B25GHT/tSuTTzXHVcAcKhaI8rDY7//puN7EZJto18GHBuM7odNXX6rYXWcn8/ihZ30Vrrf3IAMIe7Y5n99AyrX0pJRkJ2pqj6C0bKMyr/rFBJf7l4G5wZ/GexbwZ9eYF4/oMG0r6okXYC8vf0CUwPIAdaZsByP87gUh3VxaM6wzAKyuOsCM2q+oMVygUFbJw9TE2Htdm9nxUzVM6i0/mkLpoN0V70xFGHX63tiTwnnbofVxKxZNSErd3F9/PeZJl/3kVS0kxvW69Aw+f6h+DUOJfAfd1uo9Npzex5PiSSuO5d+mCR/fuZH76WbnhHt6uNLxhEAmFx5AWOzl/xDCyU0OmD2yBzS55+LvdZBSoAWCFojr5OzqNd/8+iU7A4ru60aiaXDNLq52c5TFkfHwAW24JxibehMzshlevBqVa+2e6fA+sXcW6rz6h69CRTHnzXYyuNbclpBL/CvBx8eHtQW/z1u63SC6ofH5+8KOP4tK0SYXh/e/oR6xrNtIAxYczKTqaxeM3t6ZneACpeSU88v1ebMoFhEJRLSTlFDHrB20jp8eHtKF3RGC1XMeSXkjau3sp2HgaBHjf1JSQ6Z0wBp370EgpObFzG18/8wjJJ6Jpd/0g7nljMZH9BqLT1eyqYnG1Djr26NFDRkVF1bYZZBRlEOQehM1uQ1/Jy5F2O8X79+PepUuFcXLWxlOw6hT6ADfCZnUjtdDCiLc3kmkyM2twa2YOrv7BJ4WiPmG22rnzw63sic/hxjbBfHLPddXSz1+4J43sX48jzXb0gW4E3NkG16Y+peLkpqWwdMHLIAR9bh9Pyx69Ebqqb38LIXZJKXtcKJ5q+V+AIPcgorOimfznZIqsRRXGsxcWkfCvhyk+UrEfn6Ur12ASBdiyislbl0iYrxuLxndBCFi05hibT1S/Jz+Foj4xf+VR9sTn0NDXjf/c0aXKhd9utpH18zGyfohGmu24dwoi9OGuZ4VfSkncvt0kHD6AV0Ag/cffzeTX3qJVz77VIvyXghL/i6C1f2ua+zbn2U3PVjg9U+/lSfBDD5L6+vwK4/S89SZ2pmpuJPLXJ2DNLGJAq2BmDGqFlDDz+z2k5lWvJz+For6w8mAKH2+KxaATLJ7YDX9PlwsnugQsqSbSFu+lMCoVDDr8bmtJwIRIdG7aQHLy8Wh+evHfrP3sA2xWK3qDkYhu19XavP7zUeJ/EQghmNNnDimFKXxz5JsK4/mNG4c1PZ3C7TvKDY/s1QRrYDtOW+PXc891AAAgAElEQVTAKslZdhIpJTNuakW/loFkFJh59Me9ygW0QnGFJOUU8eTP+wB4elgk3Zr6V2n+pqgU0hbvxZpWiCHYndB/dcGrpzaoazGXIKVk6y/fEdlvIFPe/C/hnbpW6fWrAtXnfwlkFGVg1BnxcfGp8OttTU9HHxRUYXjaqVwSorYStt8HWWIjcHI73NsHkpZfzLBFWv//syPact+AiOq8FYWizmK3SyZ+vJ2tMZkMigzhk3t6VFlrW1rt5Cw7iWmHthDLo3sofqNboHPRk5eexpafviXrdAITXlpQay181edfDQS5B+Hj4sMDax7gUOahcuMYgoMxbdxIzm+/lRse0syXyME3kttI2+Q95/eT2M02QrzdeP32TgDMXxnN4aS86rkJhaKO89HGGLbGZBLk5cL8sZ2qTIStOSWkvb9PE36DwH9sKwLGtUbnomf/mv/x1dMz8Q4M5PZ/z7tqunYqQ4n/JSKEYGyrscxcO5P0wvL9+hhCQ0l7YwG2vPIFvDDXzJotv2L2sGDLKSF/XQIAg9uFMrFXU8w2O4/8sIdii/L/o1BcCgdP57JgVTQAb4ztTFAVuWguPpFD2ju7sSQWoPdzJeSBLrh3C+bQ+jWYi4to1KYdd7/xDv3unIyrh2eVXLO6qRLxF0IMFUJECyFOCCGeLid8ihAiXQix1/Hvvqq4bm0xuNlgxrUexyN/P4LNXlag3dq0wevGG8h4/4Ny0wc39aZZ11FsiV8GQP6GRKxZ2kDvsyPaERHsybHUAl7782j13YRCUccoMtuY+f0eLDbJ3X2acWNkyBXnKaUkf30CGZ8c0Nwvt/Yn5OGupObG8vUzs9i/eiVFeXkENm6Cd0BQFdxFzXHF4i+E0APvAsOAdsAEIUS7cqL+IKXs4vj38ZVet7aZ1mkaT/Z8ssK5/8EzZmBJSkLa7eWGD7yrLzl4UhhYBFZJ7p/a3gDuLnreurMrBp3g8y1xrItOq7Z7UCjqEq+sOMLJdBMtQ7yYPbztFednL7GR9c0Rcv+MAwneg5oQNKU9BaZM/vfeInqNGcf4efPxDQm9cuNrgapo+fcETkgpY6SUZuB7YHQV5HtVI4Sgc3Bn/oz9k48PlP2WGUNCaLxoIbK4/KmbvsHuTFnwNM3v648w6ig6kEHxyRwAOjb25dGbtQ1gHv9pP1mm8jeMVygUGn9Hp/HVtlMY9YK3xne54j14rdnFpL+3j6KDmt993/Et2Z+5ni0/fY1vSBj/XPQhbfoMqJa+/aKCmqnvVSH+jYAEp+NEx7nzuV0IsV8I8bMQolxfCEKIaUKIKCFEVHoFfvKvNrqHduf7o9+z+lTZbSCllMTdNZHC3XvKTevl581f320jzVvbQD739xikY5rn/de3oGfzADIKSpi7rPzBZYVCoblpfvqX/QA8dnMb2je8MqdoJXG5pC3eiyXFhCHInZIbdXz/8b/JS0+j8z+GA6DTV50rBkuJjZi96az96ggZiQVYim2UFFXuUbgqqArxL+/Td/780d+BcCllJ2A18EV5GUkpP5RS9pBS9ggODq4C06qfEI8Q3hr0FvO2ziM6K7pUmBCCwHunkPr6axUu/PINC2PTwSXgpceSYjo7hUyvEywY2xl3o57f9yXxp9r/V6Eol3l/HCY1r4RuTf2YeoVTpE1RKaR/dAC7yYIxwpuQBzuTmZ/EkOkzGTHjCbwCqsYvkCm3BJvNTsLhLD57ahMH1iUS2NALDx8XfILccXWv/k3kq0L8EwHnlnxjIMk5gpQyU0p5xnXlR0D3KrjuVUP7wPa8ecObNPIq+4PHZ9QosNrIW7Gi3LTXDWuNwaMnhwu1hWF5q+KwF2rTQJsGevDM8EgAnv3tIJnK+6dCUYrVh1P5ZXcirgYdb4zrjP4y3TdIuyTnjxiyfz4ONkl+aAG/Rr1Jia2I60bdRtMOna/YVlNuCfvWJLBkwS6+fX47OSmFhLX05Z5X+zH6ka50vqkJHj5Vuwq5MqpC/HcCrYQQzYUQLsB4YJlzBCGE8z5ptwAVO8C5Rrku7DqsdivPbX6OYuu5fn6h09HgpRdxb9++3HQu7gYGTBhDtosJYzMv7IVW8tbEnw2f1KsZvSMCyDSZmaO6fxSKs+QWWpj96wEAnhjShhbBXpeVj73YSuYXhyjYdBp0cMiyjWhrFBNeWoC7t8+FM6iEnNRCdq2Mw1xkJSvJRObpAroNacY/5/cnsJEXRhd9jbTyy6NKVvgKIYYDiwA98KmU8mUhxDwgSkq5TAjxKproW4Es4AEpZaXzGK/GFb4XQkrJUxufwmq3smDgAnTi3LfVmpFB8ZEjeA0YUGH6nOhUCj4/BgJCZ3bDGKrNF07IKmTIog0Umm28e1c3RnSq/j1HFYqrnUd/2MuSPafp0cyfH+7vc1mtfltuCRmfHcKSYgJ3HX53tiStMJ6IbtddkW3xhzLZ/MsJik0WIroE02N4OJ6+VbPm4EJc7Apf5d6hiimxlTB11VS6hnRlVvdZZ8+b4+KIGz+BiOV/YAgs22+YcCSL3xe+wpBOI3BNNODayo+gf3Y4O5vgq22neO63gwR4urBq1vVVtnhFobgW+etwKlO/jMLNqGPFjAFEXEar35xsIvPzg9hyzRTYcijpDZ1vH3VZ9hRkF3N8ZxrHo1IZ/kBHbFZJYZ6ZsOY+iGrcKrI8lHuHWsJV78pbN75Fr7Bepc67hIfjO3o06YveKjdd4zb+eAX1Ze2+bxFuekqO51B85NwWjxN7NqVvi0CyTGbmLlXdP4r6S+nunsjLEv7iY9mkv78PW66ZbHsa3ndHXLLwF5ssSCk5ui2Z71/cQXaqiT63tcDD1xXfYHcatPCtceG/FJT4VwP+bv70bdSXb458w+bTm8+eD3roQUxbt2LNzCyTRugEAycOxCz9yA7WwnNXxCKt2iIxnU7w+u2d8HDRs/xAMqsPp9bMzSgUVxmv/nmE9PwSejTz596+4ZecvmBnMumfHUSW2NC38iDy+ZE06lj+mNz5WM02ju1MYfm7+/jq31soyC4hoksw977en0GT29IkMqBaN4WvSpT4VyNtA9oye9Pss1NA9T4+RKxYXm63D0DTdgEMmHgvgTdHYghyx5pRRMH2c1M8mwR48NjNbQB4bulB8ost1X8TCsVVxLaYTL7fmYCLXsdrt3e8JKGVUpK65CA5v5xASHDtHUTYvd0welTehSqlJDUuD7tdcjwqjaNbU2jZI5R7XuuHd4AbLm4G9MZrT0qvPYuvIbqFduPpnk/z8NqHzzqB07m4kP7uu+QuW1YmvhCCTje2oyDblfzm2q5h+Wviz079BJjSN5zOjX1Jzi1mwf+iy+ShUNRVii02Zi/RunsevLEFLUO8LzqttNpJ/XIflh3ZSCS+oyMIHtO20m6Zwjwze1bF8928Hfz1ySEKsopp27cBt8zoQpteYbi41c4snapCiX81M6z5MJ647gm8XM71S3r160fagjexFZjKTRO9I4kVSxeja+SmTf1ce24BtV4nePW2Tuh1gi+3nWLXqexqvweF4mpg8doTxGRovnseuKHFRafLS04l4e0tWI/kg1EQNKUD3n3Kc0IANqudmD3pmIutZCTkk5Vi4oa72jBxXm98nDZirwso8a8B/tHsH5gsJuZumYvZZsa9Sxc8+/Yl84P3y43ff1wnDK49OJi/BQQUbE3Cmnlu/+B2DX2YOiACKeGZJfsxW8t3HqdQ1BWOpuTx/vqTALx2W0dcDRd2ryCl5Ojqv4l/cxO6NInO20jI9C64RwaUiVuQXcKWX07wxTOb2bc2gcI8M03bB3LT3W1p2MrvmvDPf6ko8a8h/F39ySvJY/am2dilnZDHHkVfQd+/X6gHbQcM5UTMHoztfMB2zuvnGR4Z3IpmgR4cSy3gA0elUCjqIja75OlfDmC1Syb1bkqP8LLiXR57fl6K+KsQP0MI+kA3QqZ3xqXRuV/gdpudmL3pFOaZKco3I6Xktse7c+tj3fAL8aiu27lqUPP8a5ASWwnT/5pOZEAkT/V8CoCig4dwa9+uTMvCUmIDaUVXAikLopAWO8H3d8K1+TmnVZtPZDDx4+246HX8+ciAy17hqFBczXyxJY65yw4R6uPKX48OxMfNWGn8k7u2E+DZiKJfErHnWzA28CTonx3Qe2uuE4oLLBxYn8jhTUl4+bsx8K42BDWuO3VHzfO/CnHVu/L2oLcZ3GwwANJqJemJJyhYt65MXKOrnpw0M0ve/RxzC+0DnbP8nNdPgH4tgxjbvTFmm51nlhxQG78r6hxJOUXMX6k5A5g3ukOlwm8pLmbVh++w+8tfMX0Xhz3fgktzH4Lv74TOy0jCkSxy04swl1gx5ZoZ8VAnbn+ye50S/ktBiX8N4+3iTffQ7nx9+GuWxCwldPYzpL76GnZzWR/evsHuZCd7sHbHV+i8jVgSCyjaV9rV9b+HtyXQ04UdsVn8EJVQJg+F4lpFSsmcpQcxmW0MbR/GkPZhFce12/lx3jO457nTx2cUlEjc2gbgP6kth3ek8t0L29n883FMOSX4BLpzw11tCGp88bOF6iJK/GuJ/o36s3jvYnY2s+LasiU5P/9cJo6Lu4F+dwyixOpOdgNtVk/uyjik096+/p4uzBmlbZz26oojZCjPn4o6wqrDqaw+koa3m4EXRpe/CEtKycld20EIhgx9kOZZkWCx49IxCP2QcOxCkHg0m4ET2nDnsz1p2Mqvhu/i6kWJfy0R7hvO4kGLeX7r8+Q9Nhn/sWPLjde2X0OadbqFXK88jA08seWWkL/pdKk4t3RuyPWtg8krtvLqCrXvr+Lap8hsY97vhwF4/OY2hPq4lYljysnm19eeZ/uSH8ndGE/xnylgl2T4u7FsVzopMbm4ehgZOq0Djdr418kZO1eCEv9apH1Qe94f/D6twrtRknSalHkvltn0RacTjPjXIHqMuh1jP212UP7fidjyz3UTCSGYd0t7XAw6ftmdyPaYsu4jFIprif+uO8HpnCLaN/RhUu9mZcJzUlP46umZhDRvyfCbZlCwIh4kxLsboHsok1/uS9u+DWvB8msHJf61TNvAtggE/7f3abK2bCB/ddntIAHWfb2Pr995CkOEJ9JsI++vU6XCw4M8eWCgtvDluaUHsdjU3H/FtUlshokP1scA2iCvs6tmm9VCenwcvsEhjHxkNqEFXShYpe1/4TemBX3n9qHL4Ka15iP/WkKJ/1WAUW/k3q5TWXRjIadfnFfuyt+et7RFZ+zEvpxNoAPTzhTNB7kTD9zQ4uzc/882x5bJQ6G42pFS8vyyQ5htdsZ1b0z3Zv5nw3LTUvl+7lPsWr4UhCD5xxzcT+SAAP+xrfHqrVr6l4IS/6uEwc0GM3rcbP7X0UZxWtn9ev1CPeg4+BaiD25D19YDpDb10xk3o57nb9EGxhatPk5STlGZfBSKq5lVh1NZfywdHzcDTw2LPHs+/uA+vpn9KK6ebcnP6UPO7ydpUGgBnSBgfCSePUJr0eprEyX+VxEjIkYwecHvuDVoREZc2YHb3re0YehDzxA4ovU5n//RWaXi3NgmhGEdwig023jxj8M1ZbpCccWUGuQd0oYgL1dsViuW4mISj5rRuY4krMVArm/mjWlLMugFgRPb4tE5uJYtvzZR4n+VEegeSPSSz9hx3x2czD5RKszVw0jzLu3Yvmo3tnbaYpec5bFIW+lB4udGtsPDRc+fB1P4OzqtxmxXKK6Ed/8+N8g7sVczTh2M46N/zWTXit9p278d97x6O22lHcv+DDDoCLqnPe7ty3eRorgwSvyvQtpOmE6YT0O+fmkSJ3NK++3RGwQnohL437qP0fu7Yk0rxBSVUipOQz93HhncCoC5Sw9R7LQuQKG4GonNMPHhBq0b85n+Lfnl1SX88vJThLXsTPcRY/ALcqdw6QmK9qYjXPQE/7M9bq39L5CrojKU+F+FCJ2O9gv+y22brHwf9UmpMJ1ex033DqWo0ECWY+FX3l+nsBdbS8W7t19zWod6EZ9VyHvrlOM3xdXLmUFe/xLJnR0b0CbICw/vIm59+hnGPD4Ng15P5rdHKTqUiXDTE3RfB1wj1GKtK0WJ/1WKa0QEkb+vYPZNL5OQl8DRrHNjAM3aB9G00yiiDqzCpZk39gIL+esSS6U36nW8NKYjAO+tO0lsRvl7BygUtc2yv+MI3J3L7QVW2h74HnNhAiNnTKJ55y5Iq53Mb49SfDgT4WYg+L6OuDb1qW2T6wRK/K9ijCEh5Pz4E0k/f8v9f91PVMo5L6ejZw3h7tffwHtocwDyN53GmlNcKn3P5gHc3k1z/DZn6cEyC8gUitrEbrOTmV7I0SWxZMjTGC0/0qpbJxq01rYqLSX87gaC7+uASz33x1OVKPG/ynHv2AH/j5cxv8NsHlv/GOsT1gPaqt5TBzP57JXZGCN9wGonb2VcmfTPDI/Ex83AxuMZrDiQUiZcoahpMhLzWf7uPrb9FsNnuxN4z6OQJtYoRtz/L/rdMQmdTl+O8HdUwl/FKPG/ynFr1w6/ceNo9P5y3r3pXdwN57aSa9I2EJ2hETsS/waDoHBvOuaE/FLpg7xceXKoNl/6xT8OYyopPTagUNQka788wrK399E4MoDA6/zZ8+u3uGDm1mfm0bpnb6C8Fn/HUpuw1HVkOR5+qwMl/tcAQQ8+gEvLFrT3bUPPBj357OBnfHnoS/RGHf+YOpnjh7cg2nkCDp//53XvTOjZlI6NfEnJK+adtSfKu4RCUW3kZRZxcIPmjLB1z1AmzetN806u/PjiM3ibcxjTtfHZ3bmk1U7mN0fqnfDn/v47SbP/zckRI4kdO65GrqnE/xpA5+pKyMyZlMTGYs3IYGj4UJYcX8Ir21+hWZcGdB06GdneBZ2nAXNcHsWHSjt20+sEL47pgBDw8cYYTqTlV3AlhaLqMOWWsOH7Y/z4yk5MOSVIKWkcGQBY+Gz2Y+zWN2VLk2E8Oaoz4CT8R7LqrPBLu52CzZtJf2cx8f/8P5KfmwOANTMT904dafTGfJr/Uta9e3WgxP8aIm/FCpKfm0OYZxhfDf+KuNw4vjnyDTfePQrhFoKtvVZRcv+MRZ63qXuXJn6Mv64JVrtk7rJDavBXUW2YHdOOj+9MRacT3DW3N71uiQDg9NHD2HQuLGsylj1+XXliaCRBXq51UvillJgTE8ldtozkF14g9/ffQQiyv/4GaTbjP3kSwY/OAiBwyhT8x4/HrV07hLHybSqrCrWH7zWENJuJHT8e//Hj8b/jDix2C1JKEgsSOfDdbhK2reD2jg9iSy/Cd2QE3v0blUqfZTIz6M115BRaWHxXV0Z2Uo6wFFWH1WLjwLrT7Fl1ilsf64Z/mOfZMEtxMf/74G1yUpJIGTCVxRviaN/Qh2X/6o/OLs8Kv87DQND/XZvCL81mio8coXD3Hrz690Pn4UHs+PF4dO2Ge7eueF1/Pa4REdVuh9rDtw4iXFxoNH++1nKwWjHqjLjoXdidupt3/N7HrnMnRmiunvPWxGMvtJRKH+DpwhNDtGl0L/5xmAI1+KuoInJSC/l27naSjucwZlZp4S/IzuK7OU9gMBrp/fBcPtysuWCeN7oDOglZ3x29JoXfXlKCaccO7EVFmLbv4FjvPiTPfR5zvFYHDQ0b0mrDBhq//RaBU6bUiPBfCqrlfw0irVZw7Eok9HoA1sSv4eNf3ue6nTBx4L+xxObj1a8hfqNalEprs0tu/e9m9ifmcv/1ETwzvG2N26+oOyQczkLoBQ1a+pIWl0+DFr6lwm1WK3a7jePbNhPZ/wamfB7FhmPpjOvemPm3dyLrh2iK9qVrC7imXt3Cbzeb0bm4ULBpM5kffEDRoUO4tmhBowVvYAgJQVos6H1qfwHaxbb8lfhfo6TOfwO9jzdB06efPReTG0Pq6VN08u5K9n8PgE4QNqs7hiD3Umn3JeQw5r+b0QvBykcG0DJEzZ9WXBrp8fls/fUEeZnFXD++NU3blXWwdnDdavav/pMJLy5ACMHKgylM/3oXPm4G1jw2EP3KeAp3pSJc9QT9X4ercuVu0YED5K9ZQ+HOKEqio2m1fh2W5GQsycm4d+2G3svzwpnUMKrbp44TcPdksr78iqIDB86ei/CNoE+7G/nirfc54BYLNknun2U3dencxI/x1zXFapfMWaoGfxUXj81mR0rJtqUxNO8czIS5vcoIv91uY91Xn7B9yQ8MmT4TIQRFTi7Gn7i5NYY1iZrwG3UETWl/VQi/vaQE07ZtpC1cxOlHHwOg5NgxkNp061Yb1qPz9MS1ZUu8Bgy4KoX/UqgS8RdCDBVCRAshTgghni4n3FUI8YMjfLsQIrwqrlufMYaFETZ3LqdnPYq9qPSmLZEdwomL3UuJMFN0KJOS2Nwy6Z8c0gY/DyNbTmbyx/6ym8coFM6UFFrY/PNxfnl9FwCjHu5Mxxsao9eXlZCM+FNkJsZz18tvEti4KeDkrrmBDyOz7Ji2JYNBEHhPO1yb+5bJoyaQdjtFhw5RsF5bNX961qOkLVwIAvzu0Oba+91+OyGzHsGrnzaAW5e44m4fIYQeOAb8A0gEdgITpJSHneI8CHSSUk4XQowHbpVS3llZvqrb5+IoOnAA944dS52z22y8N20anZqMonlxIMbGXgQ/0BndeRX1ux3xPLPkAKE+rqx57Aa8XNW+p4qyxOxNZ903R2neKYiet0Tg6etabryclGRidu+g2/DRSCkRjnGp2AwTQxZuwGyzs7JbC7x2p2sbsUxuh3tkQI3dh5QSWVyMzt2d5OfmkP/XX+gDAvAZMZzghx5C2mxnx9CqG6vdSkZRBsmmZHxcfGjh14J39rzDiewTpBSm8PWwrzHqL2/K58V2+1RFbe8JnJBSxjgu/D0wGnDeRmo08Lzj75+BxUIIIVV/wxXj3rEj+WvWYElJIWDiRAB0ej033/8AJ7fvRZffAEtiAW98MZcxYybRJqDN2bR39mjC9zsT2JeQw9trjjNbDf4qnIg/lElYC198gty5ZWYXgirxrRN/cD/L355Pn9snAJwVfim1dSVmm535DYM14ddB4ITIGhF+abORt3Ilhdu2YdqyFY/evWj48sv4jBhB0L8ewhh6bvvHqhJ+KSXZJdkEuAUQlxvH5qTNJBckk1KYwr0d7sXf1Z8Rv44gwDWAMK8wbm15Ky38WtDctzmRAZE08GyATlR/j3xViH8jIMHpOBHoVVEcKaVVCJELBAIZzpGEENOAaQBNmzatAtPqB65t2pD83BzcO3TAvbO2WrJVzx60vK47h7/Yj2+emXGnBzN15QPc3fkeJrWdhF6nR6cTvDi6PaPf3cynm2IZ170xrULV4G99JyvJxOZfjpObXsSw6R0Jalz5DJyEQ5rwj5jxBE07dC4V9r9DqWw4ls49Bjf6JpWAgIA72uDeIahabJcWC0X79lGwYSOurVvjM2I4pg0bcGvfgYB77sGlhTb7zbP3+RJ1aSQVJHG64DTJpmQMwsDwiOG8vfttVsatJNWUiqfRk9XjVpNelE5cbhxhnmG0DWxLqEcoAW4B7Ji4A6OudMt+ZMTIK7LpUqmKbp9xwBAp5X2O48lATynlw05xDjniJDqOTzriZJaXJ6hun0slf/VqUl95leZLfkHvp210UVJo4oMHpjGs2QO4myXyBj8WuX3OnD5z8HbxPtu6mP3rAb7dHk+fiEC+ndrrbKtNUf8w5Zbw48s76TakGR0GNkJvqLgFarNaKcjKxCsggIKsTHxDwkqFF5ltDP7PenrmWHkMbcaZ/9hWePYIKy+7y8aSnIwwGBBGIyduHoJL48Z4DhiAz7ChuEVGXjiD87DaraQVpuHv5o/JYuKn6J84XXCaJFMSQ5oN4c7IOxn3+zjcDe409GpI5+DOTIicQGxuLAJBqGdoKQeMNU1NdvskAk2cjhsDSRXESRRCGABfIAtFleE9eDDW7Gyk/ZxbB1cPTzoOGsTubVvp59sb3ZZ85j/xKnpXF2aunUkr/1ZM6zSNJ25uw58Hktkak8nv+5O5pbNa+VufsFntHFiXSEmRlV6jIpj8Uh8MLpV3gRQV5PPHwtfwDQnl5vtnlBF+0AZ5OzsJv9/oFlUm/Nb0dDI//QzTpo1Y0zMIe34uPkOH0mLlnxgCLtydlGpKJT4/nqSCJNKL0rmv430sj1nOO3veIa0wjQC3AN668S1CPUOxSivdQrsx0mskLf1aAvDTqJ/K5Nnct3mV3FtNURUtfwPagO9NwGm0Ad+7pJSHnOI8BHR0GvC9TUp5R2X5qpb/5WFNT6dg/Xr8xo4FwFxcxCczpnN9wyn4Fhvw7BWG/62tSCtM4+VtLxOXF8dzvZ/jRHwITy85QIi3K2sfV4O/9YXY/Rls/uk4fmEe9Lu9ZamVuRWReTqB3+bPo0WP3lw/cQo6XdkPRUx6AfP/s5XZ0hUdAt8RzfEe0Piy7TQnJFCwYQOmjZsImHIPbpGRZH3zDV4DBuDWvn2Z/nqL3YLFZsHd4M53R78jPj+e+Lx4Gng24Lk+z/HC1heIyYmhoVdDGno15KEuD5FVnEWRpYgwz7DLHmy9GqjRRV5CiOHAIkAPfCqlfFkIMQ+IklIuE0K4AV8BXdFa/OPPDBBXhBL/y8OakUHsuDsIfeopfIYOASDl5HG89H7kfKBtBRkyoxsuDTyRUrI2fi1CCK5vNJBbPljO4Xg9Uwc0598j2tXmbSiqmYLsErz8Xdm7Op6Ahp7lLtKqiOTj0WQmxtPhxn+UGy6lZP7b27gz2YIBgc/NzfAZdGljeNJqpXD3btzatqX40CFOP/EEXv0H4DWgP579+6P38aHEVkJifiLxefF0DelKnjmPl7a9RHx+PGmFaczqPovJ7SazcNdCAt0CaerTlAjfCJr61O3xRLXCtx5TdPAQCVOn0vTzz3Bro83uyUo+TfRbe2iCL64RvgRN7Viqb/949nHu/vNeslK6Ys0cxJ8zBvP/7Z13eFVF+sc/c1t6SHVDLGgAACAASURBVLlJSIfQQoAAikhVEBALdrE3rOtP3FWxrmV1V9euWFdZe0WkCAqiFFF6LwkQEkgjIb3d5N7ceub3x4kiSw0EksB8nuc+cObOnfOem+Q7M++8M293tfh70mGvc7F6Ti6FmVVc9/QgLAFHNsOTUrJh3hycDTaGXn3jIesu+2kX8b8UY0ZgGhpHx/85YuRQOLOyqPrvBzQsW4YlPp7YF56nxGpkV90uCu1FlNnLeOzMx5iaNZWX175MXHAciSGJPDjgQaIDo9lYvpGk0CTiguLa9ej9WFDif4pjmzcPYbEQMno0ADWle5j2+N8ZY52ARRiIuL4ngX32jbgod5Rz83dPU9i4kR6+vzPjjnFq8fckoji7hvnvZ5I6JJYB5yfjF3hk4uj1eFj04buU5e7k0oeeJDQq+qB167ZXUvXpNiwICrsEM/j2fgf9HZJS4s7NpWrhTzT+tozEl1/h202f49m0hbWdNUITOvH88Od5Ze0rFNQXkBSSRFJIEuN7jMftc2MymDAZlHvyf1HirwCgbu5cQs45B0NAAMunfYlro53usifGMD86TjodYd7XV1rrcDNi8jRqbWHccm4V3WJNXNn9SvyMB97Yo2jbSCnZua6cDtEBhMUE0ljvpkNU83aqrp/7HUXbt3L+xAew+B88isWVV0fJf7dg0mBJIFzz+FBMRgNSSupcdbrfvTqX08uCcPXtxoyX72TQz8Vs6mYk+fwruOCqx/gg65M/XDTJoclEBx68o1EcGCX+CqSUlDz6KL4GOwlvvoHX5+XbZx7n7PCrkJUuQsckEzpqf//nN2sLeWRGBtaISs7ov4ac2h3c3EvfH6BmAu2Hsjwby77NwevxMeL6VGI6Ne/8nIqCPHxeL9GdUhBCIAwHD/t0Fdoo/28GwqMxz1xC/jkFCHMtzw59lq+yvmLhzNe5cLOJrjl2/FO6EP/eu+S4ikiM6Iw1wKp+r1oQJf4KQE8wUXjHnfh1707M3x8DwLWrlsoPMpFGQexDZ2AK23dUr2mSy/+zgk27a7l9WGcuGyRZsWcFd6TfwW9Fv9E1rCtxwSoctK0iNYmUklmvbiBtWBypg2IRhuaJa87alSx4/y3G3DGRbmcOAUCTGhWOCowGI9YAK29tfIu8ujy0EicTt16Bv9fCIr9Cvu66lPGxnemWUUOnbBuxb7yGa90GvCWlBJ99Fibr8dngpdBRp3oqAD0BTMJbbyI9bvB4EEKwYeM86oLqET5J+Yzs/T5jMAiebcr5+/GKfEzeJO5IvwOA7VXbueqHq3hgyQOsLll9oh9HcQg8bh9r5+Yx581NGIwGLn/odHoOiWuW8Ps0H79+/xXz//smIdcNo0OfruTX5XPZ7Ms488szuWbuNSwuXAxAhH8E40LG8kD2dfh7Lazy2pmMlffLejD8ie/oWiYIv/IKTMJI8JAhhF1xuRL+NoQa+Z9CeEpLcaxdh3HoYL599DFGW29EaBA2oRfBPfbfGPPkd5l8vqqAMztHMPXOQX9Mze0eO3N2zaHaWc09/e7h5/yfSYtMIyHk6OO4FcdG/pZKfv16Bx1TOjD4si6EWg/um//90LXNFZvZVrWNQlshpfZSXhzyPNOypzF99WdEhccRF9uZW3vfSkxgDPm2fBJDEgky/yk1Y4WD8nc2IJ0Se2UWBZu/omzyB1zXKxJDcDDCpBZjWwPl9lHsh7uoiIIbbiR60gMUBFqwLSigEz0xxwURPbH/fiPEOoeHka8uodru5o1r+nFJv/gDtvva+teYlTOLlA4pXNH9Ci7ucvGJeBwFUF5gIzIhmNJddQiDIK6rfrSHw+OgqKGIYHMwccFxvLjmRXLrctldv5vEkETeH/M+H2R8QElDCUmhScRoYVR+vYT0UWNJH3XeQe+nuVzYV6ygMTMXX31vfDY3db5qHqgvx5KWyncTh2FspotJ0bIo8VccEFdODgUTbiXm749RHRWF/0KJr85FbZcwet/RZ7/609bu5uEZW4gK8WPxpLMJ8T9weKDb52ZVySpsbhvjUsbx/OrniQ2KZXjCcFI6pKgFvRamvtrJ0plZFGfXYh1vp8yym4u7XIzT5+S2n26j3l1PXHAcE3pN4LJul/Hdzu+I8I8gMSSR+OB4LEbLH22V7sph9qvP0W/MBQy8dPx+Pyvp9SJMJspfn0zNl1/i33sApsTxSI8ZX3wQF+4pxY5k1v8NpV9i2In+KhT/gxJ/xUFxZmXhKSkhZORIsqf+QuAmE27AeV4n0kYk7lNX0yRXvLeCjYW13DasM0+OO7Kdvyv2rGBhwUKWFy+nc4fOvDfmPXZU78AaYCUy4Mh3k57KODwO7B47UYFRLC5czKaKTRTVF1FbYWfoqusx9WlgftiXxIfHkhiSyJXdryQ6IJoqZxXRgdFHfCzwyhlfY01MptvAIX+UeUpKqF+0mPpFC9HqG+g8/VucO3YgAsOp+aYQb2Uj5sQQHjY6+DW/huvOTOLfl+0/eFCceJT4Kw5L9Rdfkrk7F2tDOqG+CAo1SLqtNwk9wvepl1lcx8VvL0MIwdy/DiO145GHDEopqffUE2oJ5ZW1rzAzZyZh/mGc0fEMnh78NA2eBvxN/vsdb3sq4Pa5yavLY0/DHvbY95AWmUb/6P7c/OPN5NXl4fA6GJ08mheGv8DM7FmUb24k3BRJr+HxdLZ0JSjU/6jvLTWNlTO+JrlPf+JT9Q7dtWsX7t27CRkxguJJDyJMJoJHj/oji5WvwU3FlAy85Q7MsUGsGWTl3lkZRARZWDzpbMICLYe5q+JEcCJP9VS0U4LOHEjMlCls6VXBoLArSTIKQg4wGOgd34EbBiXz2coCnvpuK9/cNeiI3ThCCEItemfx4BkP8sCAB8itzaXAVoAQgi+2fcFHmR+RHJpM9/DuPHTGQxgNRmqdtcQGx7bLTsHtc1PRWEG5oxyby8bZiWezrHgZ3+/6norGCiocFbx89ssIBI8ufZS44Dhig2LpHt4dgMfOfEyfIflHIoSgZGctvpmJRErJ8Ku709F6bGkP3c5Gfnz7VRw2G/3OvZDK96dQ9913aI2NhF1+OSEjRhD/6iv7fEZzeKj8MBNvuQNTTCB+N6TyzH9WAPDo+alK+NshauR/iuMuKGDLXXdC36voKLpjTghmS4CZwZd3JTh878iyzuHhnFeXUGV3M/nqflza/8CLv0dDo7eR3NpcsmuyuTDlQtaXreeZlc9Q7ignOjCaJwc9yYCOA3h/8/tYA6xYA6x0CetCl7AuNHobsRgsGA9wsuSx4tN8OLwOgsxBNHgayK/Lp9ZVS42zhvSodOKD43lu9XPUOGuoddWSbk3nwTMe5M6f7yTflk9UYBTxwfG8dNZLbK3aSm5tLlGBUUQHRpMYnHjYs2dcDg9+gWaWTc8hKiGY7gM7Njte/3+RXi8zn3oYY3UNZ3RMJv7pp7HNm4c5MRH/3r0P2KlrTi8VH2TgKWrAZA0g6q50/vVLDp+syGdAcjjT7hqMQS3ythmU20dxxHgrK8HkT9mbm5EOjfrUCDbm13PZpNMICNk7ovt23W4emq4v/i6adDahB1n8bSk8Pg977HsI8wvDbDDz2bbPqGyspLKxkr5RfZnQewK3zL+FjeUb8TP6kRCSwMyLZzIjewZzds3BZDBhFEYeH/Q4Bgy8su4VDMKAV/NyXufzuDDlQv62+G9UOavwal6SQ5N58awXeWntS0zPno7L5yLAFMDcy+ayq3YXr69/nTD/MML9whnfYzz9ovoxPWc6EX4RhPmHERsUS1xw3D75a48Gh83N2rl55G+p5Pp/DsJkPraOTXM68VZWUtVop+GRR/EZjESOGk3o2HPxS0k59GddPio/ysRdYMMY4U/0Xelsb3D+4Qb84d5h9Ixt3s5hxfFFib+i2Sy4+wl6dhiL8DdS3MtKfk4dVzxyOsamxO+aJrnyvRVsKKzl1qGdeeqitnHssyY1nF4nDq8Da4CVUnspu+t3o0kNn+ajT1QfNKmxrnQdPunDZDCR0iGFTh06sal8ExKJSZgIsgSR0iGFBncDQggCTAEnJJfqn8nPqGTRJ9vpfmYMAy7oREDw0blTpJTYfviB+gULsa9YQfnZQ8isr+LS+x4jNq3XEbWhuX1UfbIVV24dxjA/ou5Kx9DB74/d380JAFCcOJT4K5pNVUEeBa8tIzqgE/6pQbiHphDXLQypyT/cDX9e/FWjvpZB0yQ7VpUQ2yUMS4AJj8vb7MPXQE/kU79oMYbAADpcfDGlzz6HX2oq68oLKcrZwaUPP0l47JG566RHo/KzrbhyajGEWIi+Kx2TNYCpawr/SPqz6BChv4rWQx3voGg2kcmdMY2IRJM+nFl2Is2Csjwb372+EXejF9AXf28clIxPkzw1O5O2OnhoD0gpyc+oZNpza9i+ogSfTyMw1NIs4ZceD9Lno+DGm9h14Tgca9dijNRDaaMefYTwK68goU8/rnvu1SMXfq9G1ZfbdeEPNhN1Rx9M1gCq7W5emK8nBHpiXJoS/naOEn/FPvS55Dz8B+vH6FZ+tBY5/UPCYwKY8+YmXA4PAA+c24PIIAtr82v4blNxa5rbbvG4fXicPjbML2DgRSlcNuk0IuOCD/s5KSWNW7dS8dbb5F5yKeWvvY4wGol+cBLdli0l/tVXCB46lMrCfD598B5qS0voOXwkfoGHT88IIH2S6qlZOLOqMQSaiLq9D+ZovTN6aX4WtQ4PQ7tGclF67DE9v6L1UeKv2AdhMBB1YQ/cZjfS7Ye70EjyvGexWg0snZYDQIcAM49d0BOA5+ZmYXN6WtPkdkVZno3Zkzfy29RsLAEmLn/odFL6RR1ygVhzuWj47TcaMzKQbjclTzyJ5nDQ8akniX5wEgABfftisOjrAzvXrWbavx5n0BXXENbxyEVaapLqb3fQmFmF8Ddiva0P5qacvusLqpm6djdmo+Cflxw4KkjRvlBx/or9EGYj2kALLAdD6GkE9OxAj5L5REx6GFejl0abm8v7xzN1TSHrCmp4fUE2/7joyBYRT2WWfLWDgoxKBlzQidQhhxdlX20tJU8+hX3lSvx69CDy9tsI6NOHlFkzD/4Zr5eNP87hskeeIrZrjyO2TWqSmhk5NG6qQFiMWG/tjSVen4m4vRqPzsgA4K6zutAl6vAzFEXbRy34Kg5K5nOzCauPwNI5lKg70vEUFrD5xc/JCDyLC+7pR7W/YNxbSwH44d7hpMWpxd//pabUTvaaMgZe1Jmq4gbCYgIPGLoppcSdl0fD4sXUL/6FDhdfRNhVV2GbO5egYcMwhYcfoPW9uBwOVs2cypDx12H2a97OXykltd/txL66FGE2YL21N36d924ke3NRDq8tyKazNYgf/zYc/2MMPVUcX9SCr+KY6XbPaDSzhjvPhn1tKeb4eDr3jaLHlg/54dXViF113DS4E5qEx2Zuwae1zYFEa1C1p4H5UzKZ9eoGjCYDmiaxJoTsI/ya00nD0qW4i4rxFBZSOOFW3MXFWO/+Cx0uuwxhMNDhoosOK/xVRbv58vEH8DgbEc3c7CalpO77XOyrS8EkiLw5bR/h31XRwNuLdwLw3GW9lfCfRCi3j+Kg+IUFYR2fRvVXWdTO3UVAzwisf/kLoePGETn5I6SnC/cP6shPGSVsLqrjkxX53Dasc2ub3aqUF9iwJgRTV95ITOdQzrkpFYu//mf2+yzbnZtL2Qsv0rh+PX49exI9aRKBp/Wn65Jfmu1Ld9jqmPbPxxh27U30GXlusz77u/A3rNgDRkHkjWn4d93b0Wia5LGZGbh9GuNPT2BIF5WI5WRCuX0Uh0RKSf7rv2EuN2BJ7UD0Len7vJ/x+GQ27bHyvcFGRlwKP99/FokRzY9Rb89IKSnaUcPGnwqoKXVwyX39CYvRvwPNbse+Zg32pUtp+G0pcc//G0uXLjjWrCVoyGCMoUfnKtM0H8VZ20hM64O9toagsEPPDg5k8/8Kf0Dqvgl9fs/lHBlkYZE6uK3doNw+ihZBCEHirYPQhA93Vh2OzeX7vN/rmXvp0jeKUSKRiZkreHxWxikT++/zaHg9Pkp21rH0mxy6DojhuidOw5yXQfkbb+Br0IW/+uNPMMfFkfDOOwQMGIApIoLQ88YetfA31tuY+fzTrJr5DZrmOy7CX1Hv4rm52wF46qI0JfwnIcrtozgspjA/wsZ1xfZ9HjXf7cQvJQxj05k/BpORIfeNxbq1jI/+I1i6o4JVt99L6tizCL3gQozBRxZf3p5orHeT+Vsxmb8WM3x8CvFBtVz71EBqv/2W3HtfxNKtK0FnDkJ63ISMHEnIyJEtdu/qPcXMfP4pup05lOHX3ozhKH38hxJ+gH/+sA2b08vZ3aO4uG9cS5mvaEMot4/iiJBSUvlRJq6cWkiyEH/3wP3809+u283D0zZzt00wQG4nbuN0ou66g8jbbmslq1sOKSWaT9JYVc/UFzeTEG4nPnsu5q0rsSQn02nq12h2O8JsxhgSclzu77LbMRgNFG7NoOuAM4+qjSMR/l+yypnwyVoCzMZT0o3X3lFn+yhaHG+ti9LX1oJbYhoZTsexvfd5X0rJDR+uJmtHNdcYgkkKNDHk7CASzupDwfU3ENC3LyHnjiEgPb1dJPeWUuJyeNn84UKyszzEVq4jxZtJ/Bff4M3YCD4v/unpGIOPb9y7y+FgwZS3EAYDF/71oaNqQ0pJ3Q+5NCw/tPDbXV7Off03imsbefyCntxx1qFP/VS0PZT4K44L9vVl1HybjUe6sf5fb0KSY/Z5v6DKztjJv+F0a0we2o2h/WIJifSjfO0OArb8Qv3iX/Dv0Z24F1+k4bffMEVF4detW6t2BlLTwOsFIaj+/Avs27KwZ+8iKLU7C3znE+1fS7d4F8nn9Ma/WzeE8cSFO5bn5/LD5BdITEtnxC13YLb4NbuN/YT/hp4E9DxwKs2n52zlkxX59IoLZfY9QzEZ1bJge0Nl8lIcFwJPi6ZxaxVsq6Lq2x0EPxC9T4KR5MggHhjTnX/Py+LlbUWMGZtCXYmDX36yEWodRt+nryUmTU/ybV++nIaly/CWlREyejRxL76AY8MGpNOJpUsXTFFRCEPLiI/mdOItLcVTWkZAn954ysupePNN3Hn5uAsKiHroIez9ziVjWyB7nGPod9WVpF7Vl5ukEbPfiY9t/31Q5qirZfAV19Jz+NGtG0hNUjtb38B1OOFflVvFJyvyMRkEL12ZroT/JEeN/BXNxtfgpuz19Wh2LwwMIO6S/hj+NBr2+jQufXc5mcU2bhqczD8v6Y3Pp5G7sYIti3czekIaRpMRn9dHh6hAfLW1eEpL8U9NpWbqVGxz5+HKzcVns9FjzWoc69ZT/cXnmCIiMQT4EzZ+PJZOnaj6+GOEwYB0e/BL7UHouedS9eFHuLJ34KuzgRAk/uddKt+fQuU772CKicEcE0Psc89iCA6maskKymVHwnsk0DE1mh/e2kxS70i6DYghJOLo8+MeK057Aws/eJeE1F70G3vhUbcjfZKaGdk4NpSDyaAL/wFcPQAOt5fz31hKQZWDv47qxgNjuh/1fRWti3L7KI4rjZmVVH2xHQ0fuXHZnH3vHfssAG/dU8clby/Hq0m+uv1MhnTdd4NQ7qYKlnyZRag1gM59rfQaFo9/8L5HBGtuNwaLBU95Oc6tW/FVV6M5nQQPG4bJaqXygw/ApyHMZvx7pRFyzjnYfvwRzenC2KEDxvAwAvv3R3O7ESYTjQ1ejGYDXpePH97ZjK2ikYTUCNJHJhDfo3nhkseLom2ZzHvnVbqcPpCzrp/Q7KMafkf6NKq/2UHjlkqE2UDkzb3w7xp20PrPfL+Vj5fnk9oxhDkTh2ExqVF/e0WJv+K4U/1tNo71ZdixUdG7kmE33LzP+28szOH1hdnEhwUw/77h+53/7vNpFGfVUJBZxRnjOlNV1MDmxbuJTg4lOjmEmJQO+AU03zPp82jYqhoJjQqgpsTO2h/yqSpuoLHBw5hb00jqFUlZno3o5BCMbUzklnz2X5J69yPltDOOug3p0aj6ajvO7dUIPyPWCb3w63TwpO9r8qq5espKDEIw+56h9I4/tgTxitblhIi/ECIC+AboBOQDV0kpaw5QzwdkNF0WSikvPlzbSvzbPprbR/nbG/GWN1IVUEbaI+Mw++8dqXp8Gpe/u4KM4jquHZjI85enH6I1PXdtcXYNFQX1lBfaGHBBZ8I7BjLr1Q0EhlrwCzST0i+KnkNiWTcvD3utG59Pw2Q2ctY13dm4oJCNPxfgcngJjvDnkvv6YTAISnbVEREXRHjHoDaZaLympJgFU97mvP+7n9Co6GNqS3P7qPp8G66cWkSAiahbe2NJPHjoaaPbx/lv/EZ+lYN7z+nKpHOP/CRQRdvkRIn/S0C1lPIFIcSjQLiU8pED1GuQUjYrHk6Jf/vAU2qn7O1N4NUIuawTRc5sep096o/3s8vqGffmMtw+jU8mnMGIHs0TN82nUVveSKPNjavRS1CYHzGdQslZW4bT7sFgFASGWujcNwqHzY2UksAQyz6L0G0VKSUZi39i2defMfjKa+k3dtwxnZOvOb1UfroNd14dhiAz1tv7YIk99Ca7f/2wjQ+X5dEjJoQ59w7Fz6QObmvvnCjx3wGMkFKWCCFigSVSyv2GDkr8T24aVpdQO2snmA0sa5hJyojBDLzkyj/e/8+SXbw4P4uOof78dP9ZdAhQ6f9AP6Zh7psvM+Km27EmJh9TW756N5UfZ+LZY8cQatknA9fBWLGrkus/WI1BCGb93xDSEw6+JqBoP5yos31ipJQlAE3/HmxY5y+EWCeEWCWEuPRgjQkh7myqt66iouIYTVOcKIIGdiQg3QoejbMSr2brLwtZPWvaH+/feVYK/ZPCKLU5eeb7ra1oaesjpWTLovn88MZLBISEcuXj/zpm4fdWNVL+3mY8e+yYIv2J/kvfwwp/ncPDpGmbkRImjuyqhP8U5LDiL4RYKITIPMDrkmbcJ6mpJ7oOmCyE6HKgSlLKKVLKAVLKAVFRUc1oXtGaCCEIv7wbxgh/tHIXFw6aSGi0vvlLSonRIHhlfF/8TAZmbijmx4ySVra4dagtK2X6c0+yZeF8Bl12VYu06d7TQPl7m/FVOTHHBxN1d19MRxCm+uTsTErqnPRNDGPiOV1bxBZF++Kw4i+lHC2l7H2A12ygrMndQ9O/5QdpY0/Tv7nAEqB/iz2Bok1g8DcReV0qmATuTTUkmXuQv3kDc994Ca/HQ5eoYB47PxWAR2dmUFLX2MoWnzh8Xg9SSvZkbye5Tz+ue/ZVrEmdjrldV24dFe9vQav34JfSgag7+mAMPvzpm7M3FTNn8x4CzEYmX90Ps9rMdUpyrD/1OcDv8X03A7P/t4IQIlwI4df0fyswFNh2jPdVtEEsCSGEX9oNgJrZO4kOTkbTfEx/9gkcdbXcPKQTI3tEUdfo4YFvNp8Smb92b8vgs4f/SmHGZtKGj2TgJVfusyHuaGncWkXFRxlIl4+A3pFYJ/TG4H/4sNji2kae+C4TgCfHpdHZevKduqo4Mo5V/F8AxgghcoAxTdcIIQYIIT5oqtMTWCeE2Az8ArwgpVTif5ISNCCGoMGx4JPUTt3JBbc+QELP3iz88F2EELw8vi/WYAsrc6uY8ltua5t73PC4nPz4zmvMe/tVhl19I0l9+rZY2w2r9lD1xTbwSoLO7EjEdT0R5sP/KWua5MFpm6l3ehmVGs21AxNbzCZF+0Nt8lK0ONKnUfFBBu48G+aEYKLuTEcTGh6Xk8KMTeyJ6MGEj9diMghmnmRRJh6nk+o9RUR37sKmn+fS66xzsAS0zJHIUpPUzcujYVkxACGjkggdnXTE4aHv/bqLF37MwhpsYf59Z2ENbv4hcYq2j8rkpWg1hNFA5PU9MYb74SlqoOabHRiNJhptdayY9iWNP3/GLQNi8GqSv03dhN3lbW2TjxmpaWz9dREf3X8XW39dhBCC/mPHtZjwa24fVV9u14XfIAi/sjsdxiQfsfCvL6jm5Z92APDiFelK+BVK/BXHB2OwBestvRD+Rhq3VlE3P5+IuARueGEyloAAEpf9l9SoQPIq7fxjTvsP/1z00XtsXvgjF93/KOdMuKtF2/bVu6mYsgXn1iqEvxHrrb0JGhBz+A82UWN3c+9XG/FpkjuGd2ZUzyP/rOLkRbl9FMcV584aKj/aCpok7JIuBA/WUwLWlZdRqgUy6d8fkOOXxL+uGshVZ7QfH7TUNHLWrmTDvNlc9sg/ALAEBB7TDt0D4S5uoOqzbfjqXBjD/bBO6H3YGP597JSS2z9dx6KscvolhvHtXwar6J6THHWev6JN4N81nPDLulIzI4faObswBJoI7BtNh+gYQjWNi+K8lG35hs8/LyAtdgK9E9rG6ZqHojhrGws/fBejycSQ8dcfF9EHcGwqp3p6Dng1LEkhRN6UdkShnH/mg6V5LMoqJ9TfxNvX9VfCr/gDNfJXnBBsS3Zjm58PBkHkTfumEHx8yjycy2ZSGdOLN/85kVB/03ER02OhobqKTT/PI330efi8HupKS0jue9pxsVNqkrr5eTT8pi/sBg6IIfzSrohmnkC6obCGq95biVeTTLnxdM7t1bHFbVW0PdTIX9GmCB2RiNbopeHXIqq+2E7Urb3xS9GPDn5ywlgudwSzvaSOJ6f8wMDSXzn9gkvoPngYRlPrngNUvaeYZVM/ZXfmFlKHjcBgMBDaMY7wjnHH5X6aw0PV11m4cmrBIAi7KIWgQbHN7mSqm/z8Xk1y27DOSvgV+6FG/ooThpSS2lk7sa8pRViaEox00cM8C6rsjHtrGfWNHh5O8xJVuIaq4iKu+Ps/sSYeeVTLseLzeinalknO2pWkjxpLYGgHcjeupcfg4fgFHt8NUa4CG9VfZeGrc2EIMhF5fU/8UpofBuvxadz44WpW5VbTLzGMaXcNVslZTiFUMhdFm0RqkprpempBYTYQgt6NZAAAFG1JREFUeVMa/t10P//PW0u58/P1GA2Cz28bSDdzA+Gx8eRuWMOa76bTY/AwktP7E5XUqcVy+0opqSsrJTgikvL8XGa9+AxhHWPpOmAQvc4eRXDEgfPdtiRSkzQsLabup3zQJJbEECKuS8UUfnRZvP4xO5NPVxYQFeLH9xOH0bFD66WkVJx4lPgr2ixSa5oBrC0FkyDyhr1rAC/8mMV7v+6iQ4CZ2fcMpZM1CM3nY/fWDHLWLKcwcwtj//I3QqxRbF2yEGtSMpEJyYRaozBZDr4YKqXE2VCPrbKCmM5dKMjYxIZ5synP2wXAFX//J6HRMbjsdkIirQdtp6Xx2T3UfJuNM6sagODh8XQY26nZ/v3f+WZtIY/MyMBiNPD1nYM4PbntL6ArWhYl/oo2jdQktXN2YV9VAgYIv7wbQQM64tMkd36mhyZ2iQpi5v8N3e/8fykl9VWVbF4wj8rCfKqKdzNg3OX0HXM+nz54DwAGo5H41DRG3Xo389+dzI6VSzGaTIRGx3D9c69RU1JMTUkx0Z26EBoV3SoLzM7sGmqmZ+OzuREBJiLGdycg7ehnGusLarhmyko8PslLV6S3q9BZRcuhxF/R5pFSYvspn/olRQCEjkkm5JxE7G4fV7y7gh1l9QzvZuXjW87AdAQhilJKakr2oHk9aJqGyWIhIi4Bp70Bg9GIxT/geD/SEaG5fNTNy8W+uhQAS1IIEdcevZsHoLTOyUVvL6Oi3sUtQzrx9MW9WspcRTtDib+i3dCwcg+1c3aBhMDT9bDGononl76znCq7+6QSM1deHdXfZuOrdoJREDo6mZCzEhDGo5952F1erp6yksxiG4NTIvnstoEqnv8URp3to2g3BA+OI/KGNITZgGN9GeXvbybWYOD9G0/HYjTwyYp8Pl9V0NpmHhNao5ea2TupmLIFX7UTc2wQ0RP7Ezoy8ZiE3+vTuOerDWQW20iODOSd609Twq84ItRviaJNENArkqi7+2KM8MdT1ED5Wxvp7RE8f3kfQI9g+XlraStb2XyklNg3lFH66jrsK0tAQMjIRKLv6XfY5OpH0vaTszNZsqOCiCALn0wYSERQ83YAK05dlPgr2gyWuGBiJvbDr3s4mt1L5YeZjNrj4v4RXdEk3Pv1RtbkVbe2mUeMp9ROxftbqJmWjdbgwZIcSvS9px1TNM+feWvxTr5esxs/k4H/3jRAJWZRNAsl/oo2hSHQjPWWXoSOSQaDoGH5Hq7eWs99veJweTVu+3Qt20tsrW3mIfHVuaiZkUPZGxtw59swBJkJH9+dqLvSj3m0/zufLM/jtQXZCAFvXNNPhXQqmo1a8FW0WdxF9VRP24G3vBEEbAgz8mRNLZYQC1PvHESXqODWNnEffA1uGpYWU798D3g1MEDQmbF0GJOMIbDljqn4dt1uHpq+BYAXLu/DNQOTWqxtRftHRfsoTgqkx0fdgkI9iYkmcRhgiuZkVYjgi7sG06kNuDq8tS4alhZhX1OK9GgABPSxEnpuMuaolknm8jvzMkqY+NUGNAlPXNiT24entGj7ivaPEn/FSYWn3EHtnF24dtYCUIHG9/4at/zlDJI6nvgZgJQSd14dDatKaMysgqZk9P6pEYSOSsKSGNLi95yzeQ/3f7MJnya5b3Q37hvdvcXvoWj/KPFXnHRIKXFuq6Z2QT6+UgcANiEJPD2G+BFJmK3HfxOXt9qJY0sFjg3leMt1GxD6SD9kRCKWuOPTEc1YX8RD0zejSbhnZBcePLdHmzv2WtE2UEc6K046hBAE9IrEPy2C2i0VZM3YQaJbwLpyytaVY+kcSkCalYC0CEyRLdMRSE3i2dOAM7sGZ1Y17sL6P94zhJgJOqMjQQNjMYUdv5y4X68p5O+zMpASHhjTnb+O6nbc7qU4dVDir2h3CCEI7xtNemo4z32wjuTdDkZhhjwb7jwbdXNzMVkDsCSFYEkMwRwfjCnCH0OQ+ZCjZenx4a1x4a1sxF3cgKe4AXehDc2xN8G8MBvwT4sksG8U/j3CEcdxQ5WUkjcW5TB5YQ4Aj5yXyt0juhy3+ylOLZTbR9GucXs17v9mE0syShhmsHBPQiSRZU6ky7dfXWE2YOzghzAbEGYDGAXSrSHdPrRGL1qD54D3MIb54d89HP/u4fh1D8dgMR7vx8Lj03hiVibfrNuNQcAzl/TmxkHJx/2+ivaPcvsoTgksJgNvXtuffwSZ+WJVIT8VlnDfyK78pWcs3qIG3Lvr8ZTa8da4kE4v3srGgzdmEBjD/DBF+GOOC8ISH4IlIRhjhP8J9a/XOTzcO3Ujv2VX4G828OY1/VUmLkWLo8Rf0e4xGgT/uqQ3KdZgnp27jcm/7CSn0s6LV6YTMWRvukWt0Yuv3o30aEiPD+mTGCxGhMWA8DdhDLEgDK27iJpVauOuz9dTUOUgPNDMh7ecwWlJagOXouVR4q84KRBCcOuwznSOCuLerzYyN6OE7SU23r7uNNLiQgEwBJgwBLTdX/nZm4p5dEYGjR4fveJCee+G00mMaNl9AgrF76jjHRQnFSN7RPPdPUPpERNCbqWdS99dzuerCmira1sAdY0e7v9mE3+buolGj4/LT4tnxt1DlPArjisnp/j7vKDtv+CnODXoGh3M7IlDuXZgIm6vxpPfZXLTR2vYXe1obdP2Y8WuSs6f/BuzNhbjbzbw7KW9eXV8X/zNx39RWXFqc3JG+2ybA9/eDOYg8A+FC16GrqNh6vX6tV8oJA2CvtdA1jxw1evl/mGQPBhcDaB59HoG9UfYnpmzeQ9Pzc6k1uEhwGzkwbE9uHlw8hFlBjuelNucPP9jFrM2FgPQN6EDr1/dj5Q2dl6Rov2hdvhqPl3UXTZd1M0BsGsxOG3gqoMOidB9LCx/E0q36OVSgxumw5r/wqJ/gbsezIFw43cQZIWZd4JfiN5RpF0CvS7T60pN7yhCYyFlBNhKwOsE/w56fWPLHeqlaD6VDS6enrOVH7aUAJASFcSj56UyJi3mhO+SdXp8fL6ygDcW5dDg8mIxGZg4sit3j+iikrAoWgQl/i2BpoHHDiZ/8HmgNAOcdXqHEtkF4vrD0lfBtkfvPAIj4fwXYMmLsPELvZ6rHu7LgKqdMHdS08wjBAbfC11HwU+P69d+IRCVCt1G6/fxOPfOUkI6gtrKf8ws2FbGs3O3UVClu38Gdorg7pFdGNE96rh3Ak6Pjy9XF/Ler7uoqHcBMLpnNE+N60VSpPLtK1oOJf5thd+/X08j1O3WOwNnHVi7QWg8rPrP3hlKRAoMvAMW/APyl+odiqcR7s+EdR/Con+CX9Ns4qI3ILwTzH90b4fSaTh0GwM75oP06R1HYCTEpOntCCOYTu1MT26vxlerC3hz8U6q7W4AukUHc+uwzoxLjyXEv2VnabkVDXyzdjfT1xdR1XS/XnGhTDq3O+ekxrTovRQKOEHiL4QYDzwN9AQGSikPqNZCiPOANwAj8IGU8oXDtX3SiH9L4fPunUm4bBCWBMKgC72rTu8oOqbrM4efHoeqXXtdXtd+pXccy98Ag0nvKG5boHdCPz0OfsFgCYJ+1+lrI7++rLuq/IL1DqbraCjfDm67Xs8SBKEJ+myknc5IbE4PX68u5OPl+ZTanIC+YWxkjyjGpccxtKv1qFIiSinZVdHAL1kVLNhWxpr8vZnH+sR34G+jujGqZ7Q6lE1x3DhR4t8T0ID3gQcPJP5CCCOQDYwBioC1wLVSym2HaluJ/3FASn0t4ncXlbtBdzG5G3Rhj+kN0am6+Lvq9IXv8E4w7D5Y/BzsXKjXc9vhrxsh41v44b6mDiEELnodEs6AaTeBJVh/pZytdyobv4TGan0NJSAMel8B1XlQVwSWQL08vBMYzOBt1K9PwGK7x6cxd0sJX60pZG1+NX/+c+gaHcwZncLpEhVMUkQgCeGBBPkZsZgMGA0CW6OXGoebinoX2WX1bC+xkVlso7h27y7iALORcemxXHtmEv0Tw5ToK447J9TtI4RYwsHFfzDwtJRybNP1YwBSyucP1aYS/3aAlOB1NXUI9XqHYrRAwXK943DbISwROg3TF8ar88Dj0GcVF7wMm6fChs/0MrcDxn+sL55/OLapngVGPALDJ8FH5+mdlDkQYnrBuNf1z+5erZeZA2D4g+CohOyfwOSnr9Uknqm703Yt0q9N/rqdEZ3BXqnfz+QHRj9K7ZK5maUs2FbKxsJaXF7tqL6WiCALZ3ePYmRqNCN6RBHawq4kheJQtKWzfeKB3X+6LgLOPFBFIcSdwJ0ASUkqNV2bRwgw++uvoMi95V3O2b/uwDv2L+t7jf76Xx7fs3eWQtNI+ZJ3dPH3NOqzA9AXyKXUyzwOfabgcUJNvv5Zrws6JOgzipXv6Ndep94hnPe87vLatUgv93no+EQpt/kv4baqfyA7+OEWZhb2eIZtrmguz36YBp8JlzTyqxjIVMbykOFLOhpqMZktGEJiKB/4KKd71hNftxyDyQJ1ZvDeDPUSts/ROzOjBWL76uswOxcBUi8LCIeOffSZkKtBd88ZDBCWDD637qIzmPRnNAfpHajPrZcJQ7t1vylaj8OKvxBiIXCgU6Uel1LOPoJ7HOi38oDTDSnlFGAK6CP/I2hbcbIihD6a/53IAxxlnDhQf/2ZmDQ4/8X96944a/+yy9/fv6z/DdDrUoTXhZ/XyYVBUVxoMEHJW3rH4fMwMDSOh6J7Qg7gqNJF2OgHfeMhPx+cwXp0mNvR1Dk5oHybXubz6GsuMWmw6UtorNHLIrvCRZNh/SewbbYeqqx54a5fYfcamD1Rv5Y+uOAVPdT43/H6tdQg7VK46lP4+lrIX653HKYAmLRdd7n9+kJT52GCi9/S14y+vlbvTIQRel0Kg++BWXdDbYHeoQTHwJUfwobPYeusvZ3MBa/o38XCp/eW9bkK0i7W7fQ4AKEHNYx4FNZ/qs/QhNDLz3sBqnJg3cd7v/d+10P8aTD3gb1lsX3hjNthxdtQsV0vM5j0YIddv0DG9L11B98DwdGw4Km9ZZ3Phr5X6+tdtj16WWAkjH1O/+yOefrPR2pw7rO63Quf1q+lBn2vhd6Xwzc37A0Fj0qFC1/RXaM5P++te9N3ULwefn5qb9moJ/X1sncHA0336TIKxr0G02+D/GV6mdEMD2yDtR/Cz0/qZY/k64Oq44hy+ygU7R2tSWyMJn0W5HPv7TyCo3XhclTpZdKnR5kZzVC2dW9ZcIzuCiveoLvrfp+RJA2Cyp36bOp3UUseorddsII/RC2qJ0R11zdY+tx6WWCELn4FK/QAhN/rpl8D9SWQu2TvM3QaprvnNn6+tywsGbqMhJwFen3QO5v+N0B5FhSt3Vu36yi9U932p/GotQckngHbf9CDH0Bfn0q7BEo2Q0V2U9CCQf+85oPClU0dmkHvkCO7QN5v+nvCoEfWxfXXvxNH1d66sX1112ft7r1lobF6dF71rr2dpCVY/5k0VOgbSYWxqaONapqBuvUyc8BRz+baks/fhL7gOwooRl/wvU5KufVQbSrxVygUiuZzpOJ/TFsKhRCXCSGKgMHAXCHET03lcUKIeQBSSi8wEfgJ2A5MO5zwKxQKheL4ckwLvlLKWcB+zlQp5R7ggj9dzwPmHcu9FAqFQtFyqMNEFAqF4hREib9CoVCcgijxVygUilMQJf4KhUJxCqLEX6FQKE5BlPgrFArFKUibPc9fCFEBFBxDE1agsoXMaQ3au/3Q/p9B2d/6tPdnaA37k6WUUYer1GbF/1gRQqw7kl1ubZX2bj+0/2dQ9rc+7f0Z2rL9yu2jUCgUpyBK/BUKheIU5GQW/ymtbcAx0t7th/b/DMr+1qe9P0Obtf+k9fkrFAqF4uCczCN/hUKhUBwEJf4KhUJxCnLSib8Q4jwhxA4hxE4hxKOtbU9zEUJ8JIQoF0JktrYtR4MQIlEI8YsQYrsQYqsQ4m+tbVNzEUL4CyHWCCE2Nz3DM61t09EghDAKITYKIX5obVuaixAiXwiRIYTYJIRol1mdhBBhQojpQoispr+Hwa1t0585qXz+QggjetawMeiJ4tcC10opt7WqYc1ACHEW0AB8JqXs3dr2NBchRCwQK6XcIIQIAdYDl7azn4EAgqSUDUIIM7AM+JuUclUrm9YshBAPAAOAUCnluNa2pzkIIfKBAVLKdrvBSwjxKbBUSvmBEMICBEopa1vbrt852Ub+A4GdUspcKaUbmApc0so2NQsp5W9AdWvbcbRIKUuklBua/l+Pnr0tvnWtah5Sp6Hp0tz0alejJCFEAnAh8EFr23IqIoQIBc4CPgSQUrrbkvDDySf+8cDuP10X0c6E52RCCNEJ6A+sbl1Lmk+Ty2QTUA4skFK2t2eYDDwMaK1tyFEigZ+FEOuFEHe2tjFHQQpQAXzc5Hr7QAgR1NpG/ZmTTfwPlO6+XY3YThaEEMHADOA+KaWtte1pLlJKn5SyH5AADBRCtBsXnBBiHFAupVzf2rYcA0OllKcB5wP3NLlD2xMm4DTgP1LK/oAdaFNrkCeb+BcBiX+6TgD2tJItpyxNfvIZwJdSypmtbc+x0DRVXwKc18qmNIehwMVNfvOpwDlCiC9a16Tm0ZQHHCllOXqe8IGta1GzKQKK/jRjnI7eGbQZTjbxXwt0E0J0blpguQaY08o2nVI0LZZ+CGyXUr7W2vYcDUKIKCFEWNP/A4DRQFbrWnXkSCkfk1ImSCk7of8NLJZS3tDKZh0xQoigpmABmlwl5wLtKvpNSlkK7BZC9GgqGgW0qaAHU2sb0JJIKb1CiInAT4AR+EhKubWVzWoWQoivgRGAVQhRBPxDSvlh61rVLIYCNwIZTT5zgL9LKee1ok3NJRb4tCl6zABMk1K2u3DJdkwMMEsfR2ACvpJSzm9dk46Ke4EvmwaiucCEVrZnH06qUE+FQqFQHBknm9tHoVAoFEeAEn+FQqE4BVHir1AoFKcgSvwVCoXiFESJv0KhUJyCKPFXKBSKUxAl/gqFQnEK8v9Gcz/dw2ac/AAAAABJRU5ErkJggg==\n",
+ "text/plain": [
+ "<matplotlib.figure.Figure at 0x7f1377129898>"
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
}
],
"source": [
- "x = tf.placeholder(tf.float32, [4, 2])\n",
- "w = tf.Variable([-2, -2], dtype=tf.float32)\n",
- "a = x*w\n",
- "print(x, w, a)"
+ "train_regression(\n",
+ " batch_size=10,\n",
+ " input_size=1,\n",
+ " hidden_layer_size=4,\n",
+ " output_size=1,\n",
+ " learning_rate=0.1,\n",
+ " num_steps=1000,\n",
+ " print_frequency=5\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "## Classifying MNIST digits with keras\n",
+ "\n",
+ "Softmax: https://fr.wikipedia.org/wiki/Fonction_softmax\n",
+ "\n",
+ "categorical cross-entropy cost function: Measures the probability error in discrete classification tasks in which the classes are mutually exclusive (each entry is in exactly one class).\n",
+ "\n",
+ "### using MLP\n",
+ "\n",
+ "The code comes entirely from this keras examples: https://github.com/keras-team/keras/blob/master/examples/mnist_mlp.py"
]
},
{
"cell_type": "code",
- "execution_count": 29,
+ "execution_count": 140,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "Using TensorFlow backend.\n"
+ ]
+ }
+ ],
+ "source": [
+ "import keras\n",
+ "from keras.datasets import mnist\n",
+ "from keras.models import Sequential\n",
+ "from keras.layers import Dense, Dropout\n",
+ "from keras.optimizers import RMSprop"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 142,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "# Here we declare some hyperparameters\n",
+ "batch_size = 128\n",
+ "# we have 10 class of digits 0...9\n",
+ "num_classes = 10\n",
+ "# One epoch consists of one full training cycle on the training set.\n",
+ "# Once every sample in the set is seen, you start again - marking the beginning of the 2nd epoch.\n",
+ "epochs = 20"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 151,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "# loads the data\n",
+ "def load_mnist_mlp():\n",
+ " # the data, split between train and test sets\n",
+ " (x_train, y_train), (x_test, y_test) = mnist.load_data()\n",
+ "\n",
+ " plt.imshow(x_train[0], cmap='gray')\n",
+ " plt.show()\n",
+ "\n",
+ " x_train = x_train.reshape(60000, 784)\n",
+ " x_test = x_test.reshape(10000, 784)\n",
+ " x_train = x_train.astype('float32')\n",
+ " x_test = x_test.astype('float32')\n",
+ " x_train /= 255\n",
+ " x_test /= 255\n",
+ " print(x_train.shape[0], 'train samples')\n",
+ " print(x_test.shape[0], 'test samples')\n",
+ "\n",
+ " # convert class vectors to binary class matrices\n",
+ " print(\"before categorical\", y_train.shape)\n",
+ " y_train = keras.utils.to_categorical(y_train, num_classes)\n",
+ " y_test = keras.utils.to_categorical(y_test, num_classes)\n",
+ " print(\"before categorical\", y_train.shape)\n",
+ " return x_train, y_train, x_test, y_train"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 152,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "def build_mlp_classifier():\n",
+ " model = Sequential()\n",
+ " model.add(Dense(512, activation='relu', input_shape=(784,)))\n",
+ " model.add(Dropout(0.2))\n",
+ " model.add(Dense(512, activation='relu'))\n",
+ " model.add(Dropout(0.2))\n",
+ " model.add(Dense(num_classes, activation='softmax'))\n",
+ "\n",
+ " model.summary()\n",
+ "\n",
+ " model.compile(loss='categorical_crossentropy',\n",
+ " optimizer=RMSprop(),\n",
+ " metrics=['accuracy'])\n",
+ " return model"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 153,
"metadata": {},
"outputs": [
{
"data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAP8AAAD8CAYAAAC4nHJkAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAADgpJREFUeJzt3X+MVfWZx/HPs1j+kKI4aQRCYSnEYJW4082IjSWrxkzVDQZHrekkJjQapn8wiU02ZA3/VNNgyCrslmiamaZYSFpKE3VB0iw0otLGZuKIWC0srTFsO3IDNTjywx9kmGf/mEMzxbnfe+fec++5zPN+JeT+eM6558kNnznn3O+592vuLgDx/EPRDQAoBuEHgiL8QFCEHwiK8ANBEX4gKMIPBEX4gaAIPxDUZc3cmJlxOSHQYO5u1SxX157fzO40syNm9q6ZPVrPawFoLqv12n4zmybpj5I6JQ1Jel1St7sfSqzDnh9osGbs+ZdJetfd33P3c5J+IWllHa8HoInqCf88SX8Z93goe+7vmFmPmQ2a2WAd2wKQs3o+8Jvo0OJzh/Xu3i+pX+KwH2gl9ez5hyTNH/f4y5KO1dcOgGapJ/yvS7rGzL5iZtMlfVvSrnzaAtBoNR/2u/uImfVK2iNpmqQt7v6H3DoD0FA1D/XVtDHO+YGGa8pFPgAuXYQfCIrwA0ERfiAowg8ERfiBoAg/EBThB4Ii/EBQhB8IivADQRF+ICjCDwRF+IGgCD8QFOEHgiL8QFCEHwiK8ANBEX4gKMIPBEX4gaAIPxAU4QeCIvxAUIQfCIrwA0ERfiAowg8EVfMU3ZJkZkclnZZ0XtKIu3fk0RTyM23atGT9yiuvbOj2e3t7y9Yuv/zy5LpLlixJ1tesWZOsP/XUU2Vr3d3dyXU//fTTZH3Dhg3J+uOPP56st4K6wp+5zd0/yOF1ADQRh/1AUPWG3yXtNbM3zKwnj4YANEe9h/3fcPdjZna1pF+b2f+6+/7xC2R/FPjDALSYuvb87n4suz0h6QVJyyZYpt/dO/gwEGgtNYffzGaY2cwL9yV9U9I7eTUGoLHqOeyfLekFM7vwOj939//JpSsADVdz+N39PUn/lGMvU9aCBQuS9enTpyfrN998c7K+fPnysrVZs2Yl173vvvuS9SINDQ0l65s3b07Wu7q6ytZOnz6dXPett95K1l999dVk/VLAUB8QFOEHgiL8QFCEHwiK8ANBEX4gKHP35m3MrHkba6L29vZkfd++fcl6o79W26pGR0eT9YceeihZP3PmTM3bLpVKyfqHH36YrB85cqTmbTeau1s1y7HnB4Ii/EBQhB8IivADQRF+ICjCDwRF+IGgGOfPQVtbW7I+MDCQrC9atCjPdnJVqffh4eFk/bbbbitbO3fuXHLdqNc/1ItxfgBJhB8IivADQRF+ICjCDwRF+IGgCD8QVB6z9IZ38uTJZH3t2rXJ+ooVK5L1N998M1mv9BPWKQcPHkzWOzs7k/WzZ88m69dff33Z2iOPPJJcF43Fnh8IivADQRF+ICjCDwRF+IGgCD8QFOEHgqr4fX4z2yJphaQT7r40e65N0g5JCyUdlfSAu6d/6FxT9/v89briiiuS9UrTSff19ZWtPfzww8l1H3zwwWR9+/btyTpaT57f5/+ppDsveu5RSS+5+zWSXsoeA7iEVAy/u++XdPElbCslbc3ub5V0T859AWiwWs/5Z7t7SZKy26vzawlAMzT82n4z65HU0+jtAJicWvf8x81sriRltyfKLeju/e7e4e4dNW4LQAPUGv5dklZl91dJ2plPOwCapWL4zWy7pN9JWmJmQ2b2sKQNkjrN7E+SOrPHAC4hFc/53b27TOn2nHsJ69SpU3Wt/9FHH9W87urVq5P1HTt2JOujo6M1bxvF4go/ICjCDwRF+IGgCD8QFOEHgiL8QFBM0T0FzJgxo2ztxRdfTK57yy23JOt33XVXsr53795kHc3HFN0Akgg/EBThB4Ii/EBQhB8IivADQRF+ICjG+ae4xYsXJ+sHDhxI1oeHh5P1l19+OVkfHBwsW3vmmWeS6zbz/+ZUwjg/gCTCDwRF+IGgCD8QFOEHgiL8QFCEHwiKcf7gurq6kvVnn302WZ85c2bN2163bl2yvm3btmS9VCrVvO2pjHF+AEmEHwiK8ANBEX4gKMIPBEX4gaAIPxBUxXF+M9siaYWkE+6+NHvuMUmrJf01W2ydu/+q4sYY57/kLF26NFnftGlTsn777bXP5N7X15esr1+/Pll///33a972pSzPcf6fSrpzguf/093bs38Vgw+gtVQMv7vvl3SyCb0AaKJ6zvl7zez3ZrbFzK7KrSMATVFr+H8kabGkdkklSRvLLWhmPWY2aGblf8wNQNPVFH53P+7u5919VNKPJS1LLNvv7h3u3lFrkwDyV1P4zWzuuIddkt7Jpx0AzXJZpQXMbLukWyV9ycyGJH1f0q1m1i7JJR2V9N0G9gigAfg+P+oya9asZP3uu+8uW6v0WwFm6eHqffv2JeudnZ3J+lTF9/kBJBF+ICjCDwRF+IGgCD8QFOEHgmKoD4X57LPPkvXLLktfhjIyMpKs33HHHWVrr7zySnLdSxlDfQCSCD8QFOEHgiL8QFCEHwiK8ANBEX4gqIrf50dsN9xwQ7J+//33J+s33nhj2VqlcfxKDh06lKzv37+/rtef6tjzA0ERfiAowg8ERfiBoAg/EBThB4Ii/EBQjPNPcUuWLEnWe3t7k/V77703WZ8zZ86ke6rW+fPnk/VSqZSsj46O5tnOlMOeHwiK8ANBEX4gKMIPBEX4gaAIPxAU4QeCqjjOb2bzJW2TNEfSqKR+d/+hmbVJ2iFpoaSjkh5w9w8b12pclcbSu7u7y9YqjeMvXLiwlpZyMTg4mKyvX78+Wd+1a1ee7YRTzZ5/RNK/uftXJX1d0hozu07So5JecvdrJL2UPQZwiagYfncvufuB7P5pSYclzZO0UtLWbLGtku5pVJMA8jepc34zWyjpa5IGJM1295I09gdC0tV5Nwegcaq+tt/MvijpOUnfc/dTZlVNByYz65HUU1t7ABqlqj2/mX1BY8H/mbs/nz193MzmZvW5kk5MtK6797t7h7t35NEwgHxUDL+N7eJ/Iumwu28aV9olaVV2f5Wknfm3B6BRKk7RbWbLJf1G0tsaG+qTpHUaO+//paQFkv4s6VvufrLCa4Wconv27NnJ+nXXXZesP/3008n6tddeO+me8jIwMJCsP/nkk2VrO3em9xd8Jbc21U7RXfGc391/K6nci90+maYAtA6u8AOCIvxAUIQfCIrwA0ERfiAowg8ExU93V6mtra1sra+vL7lue3t7sr5o0aKaesrDa6+9lqxv3LgxWd+zZ0+y/sknn0y6JzQHe34gKMIPBEX4gaAIPxAU4QeCIvxAUIQfCCrMOP9NN92UrK9duzZZX7ZsWdnavHnzauopLx9//HHZ2ubNm5PrPvHEE8n62bNna+oJrY89PxAU4QeCIvxAUIQfCIrwA0ERfiAowg8EFWacv6urq656PQ4dOpSs7969O1kfGRlJ1lPfuR8eHk6ui7jY8wNBEX4gKMIPBEX4gaAIPxAU4QeCIvxAUObu6QXM5kvaJmmOpFFJ/e7+QzN7TNJqSX/NFl3n7r+q8FrpjQGom7tbNctVE/65kua6+wEzmynpDUn3SHpA0hl3f6rapgg/0HjVhr/iFX7uXpJUyu6fNrPDkor96RoAdZvUOb+ZLZT0NUkD2VO9ZvZ7M9tiZleVWafHzAbNbLCuTgHkquJh/98WNPuipFclrXf3581stqQPJLmkH2js1OChCq/BYT/QYLmd80uSmX1B0m5Je9x90wT1hZJ2u/vSCq9D+IEGqzb8FQ/7zcwk/UTS4fHBzz4IvKBL0juTbRJAcar5tH+5pN9IeltjQ32StE5St6R2jR32H5X03ezDwdRrsecHGizXw/68EH6g8XI77AcwNRF+ICjCDwRF+IGgCD8QFOEHgiL8QFCEHwiK8ANBEX4gKMIPBEX4gaAIPxAU4QeCavYU3R9I+r9xj7+UPdeKWrW3Vu1Lorda5dnbP1a7YFO/z/+5jZsNuntHYQ0ktGpvrdqXRG+1Kqo3DvuBoAg/EFTR4e8vePsprdpbq/Yl0VutCumt0HN+AMUpes8PoCCFhN/M7jSzI2b2rpk9WkQP5ZjZUTN728wOFj3FWDYN2gkze2fcc21m9msz+1N2O+E0aQX19piZvZ+9dwfN7F8L6m2+mb1sZofN7A9m9kj2fKHvXaKvQt63ph/2m9k0SX+U1ClpSNLrkrrd/VBTGynDzI5K6nD3wseEzexfJJ2RtO3CbEhm9h+STrr7huwP51Xu/u8t0ttjmuTMzQ3qrdzM0t9Rge9dnjNe56GIPf8ySe+6+3vufk7SLyStLKCPlufu+yWdvOjplZK2Zve3auw/T9OV6a0luHvJ3Q9k909LujCzdKHvXaKvQhQR/nmS/jLu8ZBaa8pvl7TXzN4ws56im5nA7AszI2W3Vxfcz8UqztzcTBfNLN0y710tM17nrYjwTzSbSCsNOXzD3f9Z0l2S1mSHt6jOjyQt1tg0biVJG4tsJptZ+jlJ33P3U0X2Mt4EfRXyvhUR/iFJ88c9/rKkYwX0MSF3P5bdnpD0gsZOU1rJ8QuTpGa3Jwru52/c/bi7n3f3UUk/VoHvXTaz9HOSfubuz2dPF/7eTdRXUe9bEeF/XdI1ZvYVM5su6duSdhXQx+eY2YzsgxiZ2QxJ31TrzT68S9Kq7P4qSTsL7OXvtMrMzeVmllbB712rzXhdyEU+2VDGf0maJmmLu69vehMTMLNFGtvbS2PfePx5kb2Z2XZJt2rsW1/HJX1f0n9L+qWkBZL+LOlb7t70D97K9HarJjlzc4N6Kzez9IAKfO/ynPE6l364wg+IiSv8gKAIPxAU4QeCIvxAUIQfCIrwA0ERfiAowg8E9f/Ex0YKZYOZcwAAAABJRU5ErkJggg==\n",
"text/plain": [
- "array([[-0., -0.],\n",
- " [-0., -2.],\n",
- " [-2., -0.],\n",
- " [-2., -2.]], dtype=float32)"
+ "<matplotlib.figure.Figure at 0x7f1374edbe10>"
]
},
- "execution_count": 29,
"metadata": {},
- "output_type": "execute_result"
+ "output_type": "display_data"
+ },
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "60000 train samples\n",
+ "10000 test samples\n",
+ "before categorical (60000,)\n",
+ "before categorical (60000, 10)\n",
+ "_________________________________________________________________\n",
+ "Layer (type) Output Shape Param # \n",
+ "=================================================================\n",
+ "dense_1 (Dense) (None, 512) 401920 \n",
+ "_________________________________________________________________\n",
+ "dropout_1 (Dropout) (None, 512) 0 \n",
+ "_________________________________________________________________\n",
+ "dense_2 (Dense) (None, 512) 262656 \n",
+ "_________________________________________________________________\n",
+ "dropout_2 (Dropout) (None, 512) 0 \n",
+ "_________________________________________________________________\n",
+ "dense_3 (Dense) (None, 10) 5130 \n",
+ "=================================================================\n",
+ "Total params: 669,706\n",
+ "Trainable params: 669,706\n",
+ "Non-trainable params: 0\n",
+ "_________________________________________________________________\n",
+ "Train on 60000 samples, validate on 10000 samples\n",
+ "Epoch 1/20\n",
+ "60000/60000 [==============================] - 4s 62us/step - loss: 0.2488 - acc: 0.9238 - val_loss: 0.0978 - val_acc: 0.9695\n",
+ "Epoch 2/20\n",
+ "60000/60000 [==============================] - 2s 39us/step - loss: 0.1036 - acc: 0.9690 - val_loss: 0.0796 - val_acc: 0.9759\n",
+ "Epoch 3/20\n",
+ "60000/60000 [==============================] - 2s 38us/step - loss: 0.0744 - acc: 0.9776 - val_loss: 0.0764 - val_acc: 0.9788\n",
+ "Epoch 4/20\n",
+ "60000/60000 [==============================] - 2s 38us/step - loss: 0.0604 - acc: 0.9818 - val_loss: 0.0695 - val_acc: 0.9806\n",
+ "Epoch 5/20\n",
+ "60000/60000 [==============================] - 2s 38us/step - loss: 0.0484 - acc: 0.9848 - val_loss: 0.0769 - val_acc: 0.9800\n",
+ "Epoch 6/20\n",
+ "60000/60000 [==============================] - 2s 39us/step - loss: 0.0438 - acc: 0.9867 - val_loss: 0.0737 - val_acc: 0.9817\n",
+ "Epoch 7/20\n",
+ "60000/60000 [==============================] - 2s 39us/step - loss: 0.0369 - acc: 0.9890 - val_loss: 0.0793 - val_acc: 0.9826\n",
+ "Epoch 8/20\n",
+ "60000/60000 [==============================] - 2s 38us/step - loss: 0.0355 - acc: 0.9898 - val_loss: 0.0777 - val_acc: 0.9811\n",
+ "Epoch 9/20\n",
+ "60000/60000 [==============================] - 2s 38us/step - loss: 0.0306 - acc: 0.9909 - val_loss: 0.0873 - val_acc: 0.9799\n",
+ "Epoch 10/20\n",
+ "60000/60000 [==============================] - 2s 38us/step - loss: 0.0273 - acc: 0.9925 - val_loss: 0.1029 - val_acc: 0.9813\n",
+ "Epoch 11/20\n",
+ "60000/60000 [==============================] - 2s 39us/step - loss: 0.0267 - acc: 0.9925 - val_loss: 0.0852 - val_acc: 0.9851\n",
+ "Epoch 12/20\n",
+ "60000/60000 [==============================] - 2s 38us/step - loss: 0.0244 - acc: 0.9933 - val_loss: 0.0984 - val_acc: 0.9806\n",
+ "Epoch 13/20\n",
+ "60000/60000 [==============================] - 2s 39us/step - loss: 0.0225 - acc: 0.9933 - val_loss: 0.1077 - val_acc: 0.9814\n",
+ "Epoch 14/20\n",
+ "60000/60000 [==============================] - 2s 39us/step - loss: 0.0230 - acc: 0.9935 - val_loss: 0.1030 - val_acc: 0.9820\n",
+ "Epoch 15/20\n",
+ "60000/60000 [==============================] - 2s 39us/step - loss: 0.0234 - acc: 0.9937 - val_loss: 0.0993 - val_acc: 0.9843\n",
+ "Epoch 16/20\n",
+ "60000/60000 [==============================] - 2s 39us/step - loss: 0.0215 - acc: 0.9945 - val_loss: 0.1102 - val_acc: 0.9828\n",
+ "Epoch 17/20\n",
+ "60000/60000 [==============================] - 2s 39us/step - loss: 0.0178 - acc: 0.9954 - val_loss: 0.1087 - val_acc: 0.9828\n",
+ "Epoch 18/20\n",
+ "60000/60000 [==============================] - 2s 39us/step - loss: 0.0171 - acc: 0.9955 - val_loss: 0.1187 - val_acc: 0.9826\n",
+ "Epoch 19/20\n",
+ "60000/60000 [==============================] - 2s 39us/step - loss: 0.0195 - acc: 0.9952 - val_loss: 0.1260 - val_acc: 0.9810\n",
+ "Epoch 20/20\n",
+ "60000/60000 [==============================] - 2s 38us/step - loss: 0.0191 - acc: 0.9950 - val_loss: 0.1141 - val_acc: 0.9845\n",
+ "Test loss: 0.11406206586321478\n",
+ "Test accuracy: 0.9845\n"
+ ]
+ }
+ ],
+ "source": [
+ "def train_mlp_classifier():\n",
+ " x_train, y_train, x_test, y_train = load_mnist_mlp()\n",
+ " model = build_mlp_classifier()\n",
+ " history = model.fit(x_train, y_train,\n",
+ " batch_size=batch_size,\n",
+ " epochs=epochs,\n",
+ " verbose=1,\n",
+ " validation_data=(x_test, y_test))\n",
+ " score = model.evaluate(x_test, y_test, verbose=0)\n",
+ " print('Test loss:', score[0])\n",
+ " print('Test accuracy:', score[1])\n",
+ "\n",
+ "train_mlp_classifier()"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "### using MLP\n",
+ "\n",
+ "The code comes entirely from this keras examples: https://github.com/keras-team/keras/blob/master/examples/mnist_cnn.py"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 154,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "import keras\n",
+ "from keras.datasets import mnist\n",
+ "from keras.models import Sequential\n",
+ "from keras.layers import Dense, Dropout, Flatten\n",
+ "from keras.layers import Conv2D, MaxPooling2D\n",
+ "from keras import backend as K"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 155,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "batch_size = 128\n",
+ "num_classes = 10\n",
+ "epochs = 12"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 157,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "def load_mnist_cnn():\n",
+ " # input image dimensions\n",
+ " img_rows, img_cols = 28, 28\n",
+ "\n",
+ " # the data, split between train and test sets\n",
+ " (x_train, y_train), (x_test, y_test) = mnist.load_data()\n",
+ "\n",
+ " if K.image_data_format() == 'channels_first':\n",
+ " x_train = x_train.reshape(x_train.shape[0], 1, img_rows, img_cols)\n",
+ " x_test = x_test.reshape(x_test.shape[0], 1, img_rows, img_cols)\n",
+ " input_shape = (1, img_rows, img_cols)\n",
+ " else:\n",
+ " x_train = x_train.reshape(x_train.shape[0], img_rows, img_cols, 1)\n",
+ " x_test = x_test.reshape(x_test.shape[0], img_rows, img_cols, 1)\n",
+ " input_shape = (img_rows, img_cols, 1)\n",
+ "\n",
+ " x_train = x_train.astype('float32')\n",
+ " x_test = x_test.astype('float32')\n",
+ " x_train /= 255\n",
+ " x_test /= 255\n",
+ " print('x_train shape:', x_train.shape)\n",
+ " print(x_train.shape[0], 'train samples')\n",
+ " print(x_test.shape[0], 'test samples')\n",
+ "\n",
+ " # convert class vectors to binary class matrices\n",
+ " y_train = keras.utils.to_categorical(y_train, num_classes)\n",
+ " y_test = keras.utils.to_categorical(y_test, num_classes)\n",
+ " return input_shape, x_train, y_train, x_test, y_train"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 165,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "def build_cnn_classifier(input_shape):\n",
+ " model = Sequential()\n",
+ " model.add(Conv2D(32, kernel_size=(3, 3),\n",
+ " activation='relu',\n",
+ " input_shape=input_shape))\n",
+ " model.add(Conv2D(64, (3, 3), activation='relu'))\n",
+ " model.add(MaxPooling2D(pool_size=(2, 2)))\n",
+ " model.add(Dropout(0.25))\n",
+ " model.add(Flatten())\n",
+ " model.add(Dense(128, activation='relu'))\n",
+ " model.add(Dropout(0.5))\n",
+ " model.add(Dense(num_classes, activation='softmax'))\n",
+ "\n",
+ " model.compile(loss=keras.losses.categorical_crossentropy,\n",
+ " optimizer=keras.optimizers.Adadelta(),\n",
+ " metrics=['accuracy'])\n",
+ " model.summary()\n",
+ " return model"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 164,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "x_train shape: (60000, 28, 28, 1)\n",
+ "60000 train samples\n",
+ "10000 test samples\n",
+ "Train on 60000 samples, validate on 10000 samples\n",
+ "Epoch 1/12\n",
+ "60000/60000 [==============================] - 14s 239us/step - loss: 0.2570 - acc: 0.9208 - val_loss: 0.0548 - val_acc: 0.9827\n",
+ "Epoch 2/12\n",
+ "60000/60000 [==============================] - 10s 163us/step - loss: 0.0836 - acc: 0.9756 - val_loss: 0.0390 - val_acc: 0.9867\n",
+ "Epoch 3/12\n",
+ "60000/60000 [==============================] - 10s 163us/step - loss: 0.0622 - acc: 0.9816 - val_loss: 0.0365 - val_acc: 0.9882\n",
+ "Epoch 4/12\n",
+ "60000/60000 [==============================] - 10s 165us/step - loss: 0.0517 - acc: 0.9846 - val_loss: 0.0332 - val_acc: 0.9889\n",
+ "Epoch 5/12\n",
+ "60000/60000 [==============================] - 10s 164us/step - loss: 0.0457 - acc: 0.9867 - val_loss: 0.0299 - val_acc: 0.9897\n",
+ "Epoch 6/12\n",
+ "60000/60000 [==============================] - 10s 164us/step - loss: 0.0400 - acc: 0.9881 - val_loss: 0.0270 - val_acc: 0.9905\n",
+ "Epoch 7/12\n",
+ "60000/60000 [==============================] - 10s 166us/step - loss: 0.0359 - acc: 0.9887 - val_loss: 0.0297 - val_acc: 0.9908\n",
+ "Epoch 8/12\n",
+ "60000/60000 [==============================] - 10s 165us/step - loss: 0.0331 - acc: 0.9899 - val_loss: 0.0300 - val_acc: 0.9904\n",
+ "Epoch 9/12\n",
+ "60000/60000 [==============================] - 10s 164us/step - loss: 0.0305 - acc: 0.9906 - val_loss: 0.0299 - val_acc: 0.9904\n",
+ "Epoch 10/12\n",
+ "60000/60000 [==============================] - 10s 166us/step - loss: 0.0280 - acc: 0.9910 - val_loss: 0.0260 - val_acc: 0.9916\n",
+ "Epoch 11/12\n",
+ "60000/60000 [==============================] - 10s 165us/step - loss: 0.0255 - acc: 0.9922 - val_loss: 0.0256 - val_acc: 0.9917\n",
+ "Epoch 12/12\n",
+ "60000/60000 [==============================] - 10s 165us/step - loss: 0.0247 - acc: 0.9925 - val_loss: 0.0279 - val_acc: 0.9925\n",
+ "Test loss: 0.02789461574091515\n",
+ "Test accuracy: 0.9925\n"
+ ]
}
],
"source": [
- "sess.run(a, feed_dict={x: [[0, 0], [0, 1], [1, 0], [1, 1]]})"
+ "def train_cnn_classifier():\n",
+ " input_shape, x_train, y_train, x_test, y_train = load_mnist_cnn()\n",
+ " model = build_cnn_classifier(input_shape)\n",
+ " model.fit(x_train, y_train,\n",
+ " batch_size=batch_size,\n",
+ " epochs=epochs,\n",
+ " verbose=1,\n",
+ " validation_data=(x_test, y_test))\n",
+ " score = model.evaluate(x_test, y_test, verbose=0)\n",
+ " print('Test loss:', score[0])\n",
+ " print('Test accuracy:', score[1])\n",
+ "train_cnn_classifier()"
]
},
{
diff --git a/README.md b/README.md
index c0eed22f39d95142f864eb772767820d36827e7b..6e381090a8c529a9cee73ee14f3d09ec370a94c5 100644
--- a/README.md
+++ b/README.md
@@ -35,6 +35,7 @@ In order to launch jobs on IGRIDA, you need to submit jobs using the `oarsub` co
oarsub -S -t timesharing -l /nodes=1/core=4/gpu_device=1,walltime=01:30:0 scripts/run_igrida_staller.sh
# connect to it using the OAR_JOB_ID, you can list your jobs with oarstat -u
oarsub -C JOB_ID
+oarsub -I -t timesharing -p "host = 'igrida-abacus.irisa.fr'" -l /nodes=1/core=4,walltime=40:00:0
```
You can find the script `scripts/run_igrida_staller.sh` [here](scripts/run_igrida_staller.sh).
diff --git a/scripts/run_igrida_staller.sh b/scripts/run_igrida_staller.sh
new file mode 100755
index 0000000000000000000000000000000000000000..fa5be95679f38a80e9d11da825f5c6aac2269559
--- /dev/null
+++ b/scripts/run_igrida_staller.sh
@@ -0,0 +1,36 @@
+#!/bin/bash
+set -xv
+set -e
+
+echo
+echo OAR_WORKDIR : $OAR_WORKDIR
+echo
+echo "cat \$OAR_NODE_FILE :"
+cat $OAR_NODE_FILE
+echo
+
+echo "
+##########################################################################
+# Where will your run take place ?
+#
+# * It is NOT recommanded to run in $HOME/... (especially to write),
+# but rather in /temp_dd/igrida-fs1/...
+# Writing directly somewhere in $HOME/... will necessarily cause NFS problems at some time.
+# Please respect this policy.
+#
+# * The program to run may be somewhere in your $HOME/... however
+#
+##########################################################################
+"
+
+#source /udd/kchoi/prog/utils/set_env.sh
+
+echo "=============== RUN ==============="
+
+echo "Running ..."
+
+sleep 54000
+
+echo
+echo OK
+